Предмет: Геометрия
Автор: NeverLove
Вопрос задан 8 лет назад

Задание №35:
Найдите острый угол, если отношение периметра ромба к сумме диагоналей равно $sqrt{3}$ .
А) $30^{0}$
Б) $arcsin frac{1}{3}$
В) $45^{0}$
Г) $60^{0}$
Д) $arccos frac{1}{3}$

Ответы

Ответ дал: Artem112

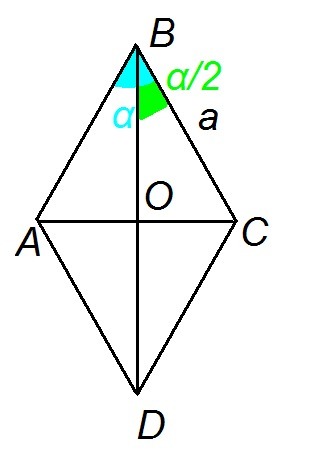
Пусть а - сторона ромба ABCD, α - искомый острый угол. Диагонали ромба AC и BD делят его на 4 равных треугольника. Рассмотрим треугольник ВОС: угол ВОС=α/2, так как диагонали ромба являются биссектрисами углов. Выражаем катеты через тригонометрические функции и гипотенузу - сторону ромба, обозначенную за а:
$BO=acosfrac{ alpha }{2} \ CO=asinfrac{ alpha }{2}$
Так как диагонали точкой пересечения делятся пополам, то сами диагонали будут равны $2acos frac{alpha }{2}$ и $2asin frac{alpha }{2}$ . Периметр ромба равен $4a$ .
Составляем заданное отношение:
$dfrac{4a}{2asin frac{ alpha }{2} +2acos frac{ alpha }{2} } = sqrt{3} \ dfrac{2}{sin frac{ alpha }{2}+cos frac{ alpha }{2}} = sqrt{3} \ sin frac{ alpha }{2}+cos frac{ alpha }{2}= frac{2}{ sqrt{3} } \ sin^2 frac{ alpha }{2}+cos^2 frac{ alpha }{2}+2sin frac{ alpha }{2}cos frac{ alpha }{2}=(frac{2}{ sqrt{3} } )^2 \ 1+sin alpha = frac{4}{ 3 } \ sin alpha = frac{1}{ 3 } \ alpha=arcsin frac{1}{ 3 }$
Ответ: arcsin(1/3)

Приложения: