Медиана CD треугольника ABC делит его на два треугольника. Докажите, что площадь треугольника ABC вдвое больше, чем площадь треугольника ACD

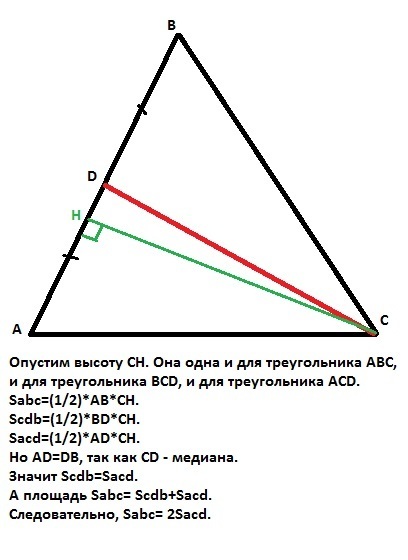
Опустим высоту СН. Она одна и для треугольника АВС, и для треугольника ВСD, и для треугольника АСD.
Sabc=(1/2)*AB*CH.
Scdb=(1/2)*BD*CH.
Sacd=(1/2)*AD*CH.
Но AD=DB, так как СD - медиана.
Значит Scdb=Sacd.
А площадь Sabc= Scdb+Sacd.
Следовательно, Sabc= 2Sacd. Что и требовалось доказать.