Ответы
Ответ дал:
0
Четырехугольник является прямоугольником, если его диагонали равны.
По данной формуле вычислим длины диагоналей:



Диагонали данного четырехугольника не равны, значит он не является прямоугольником
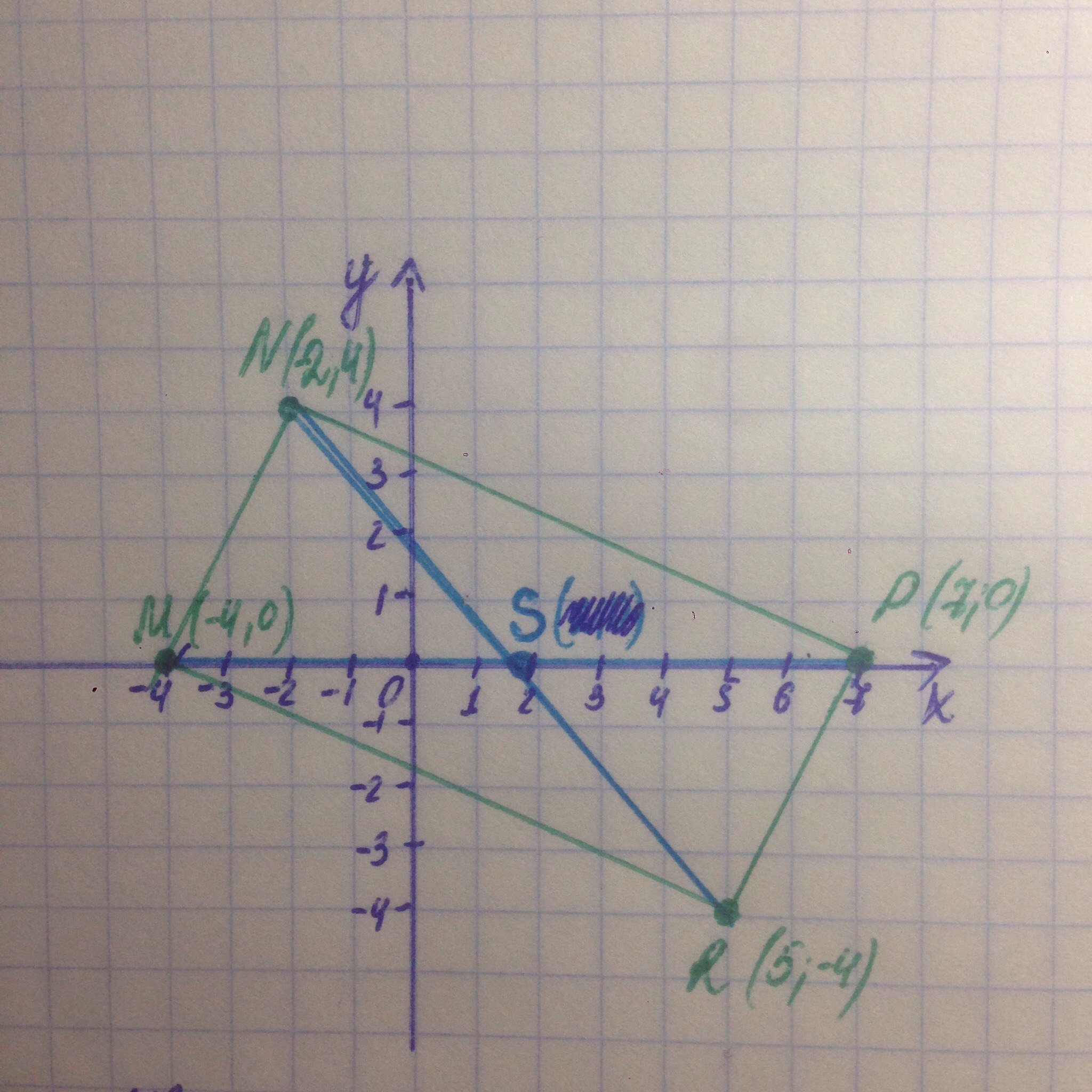
Найдем точку пересечения S диагоналей по формуле середины отрезков:


NP (1.5, 0)


MP (1.5 , 0)


Координаты точки пересечения S = (1.5, 0)
По данной формуле вычислим длины диагоналей:
Диагонали данного четырехугольника не равны, значит он не является прямоугольником
Найдем точку пересечения S диагоналей по формуле середины отрезков:
NP (1.5, 0)
MP (1.5 , 0)
Координаты точки пересечения S = (1.5, 0)
Приложения:
Похожие вопросы
2 года назад
9 лет назад
9 лет назад
