Найдите диагонали ромба, если его сторона равна a, а один из углов 120 гр.

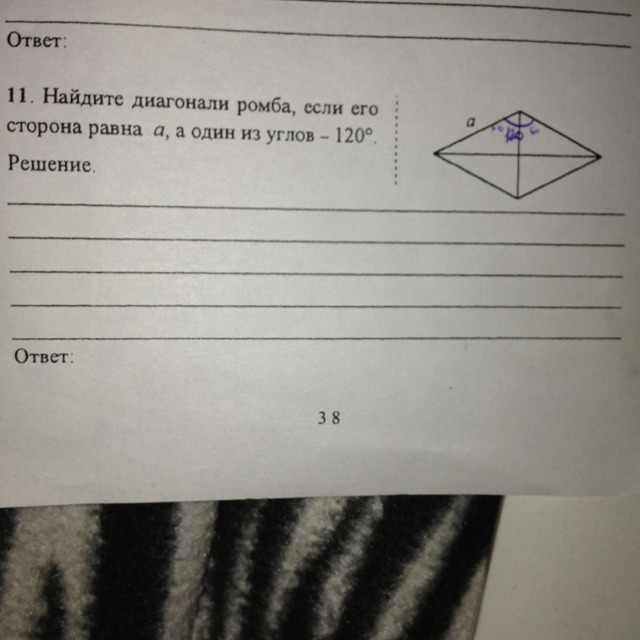
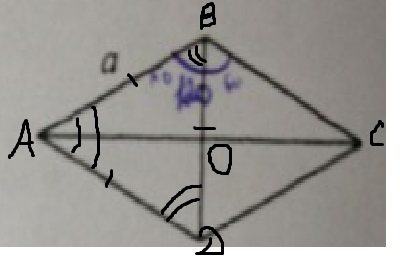
Обозначим точку пересечения диагоналей как O.

Тогда рассмотрим треугольник DAB: 
Т.к. дан ромб, то DA=AB=a;

Т.к. дан угол B 120⁰, то угол ABD=60⁰ и равен углу BDA, значит третий угол найдем по формуле 180⁰-60⁰-60⁰=60⁰ - значит треугольник DAB - равносторонний.

Высота равностороннего треугольника (AO) равна:  

Значит вся диагональ (AC) равна: 

А другая диагональ равна  потому что треугольник DAB - равносторонний.

Ответ: