народ,поможете?
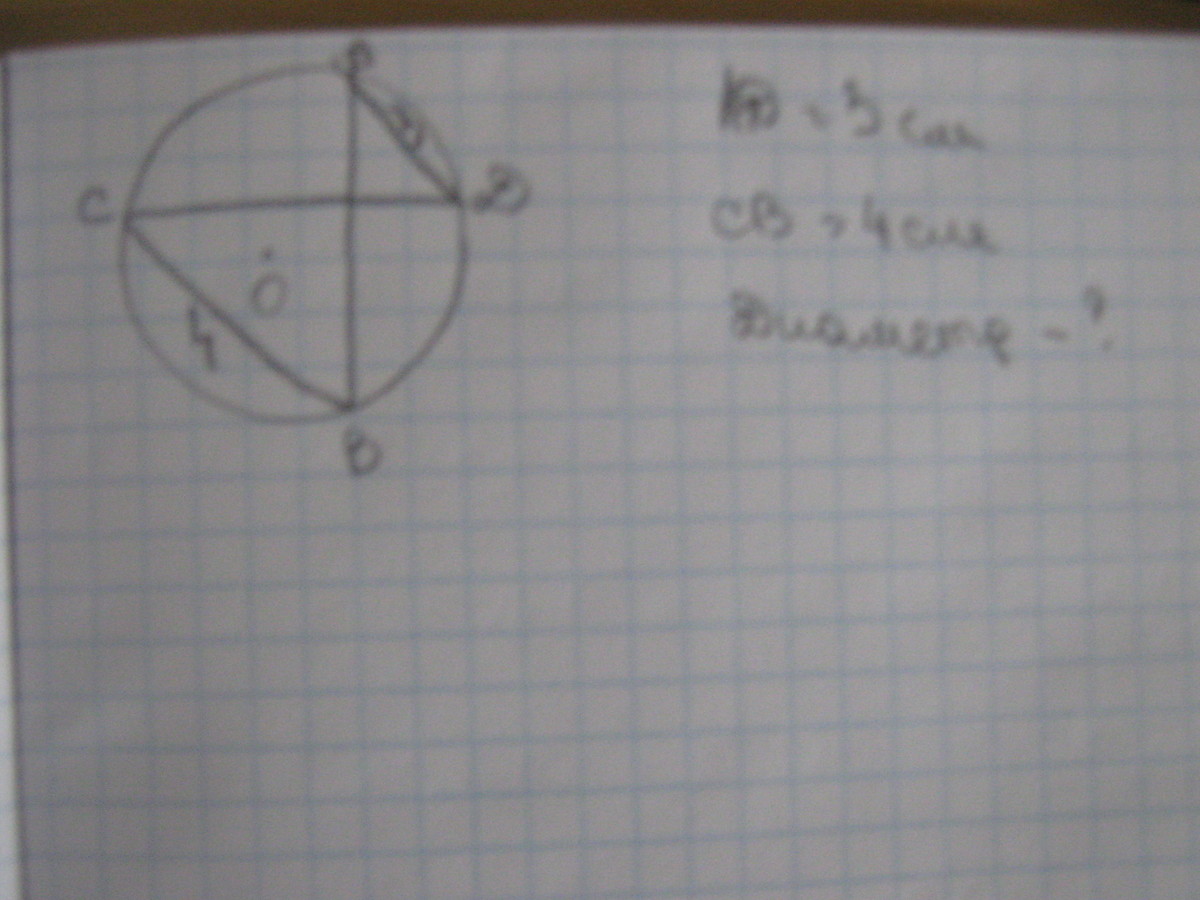
в окружности проведены две взаимно перпендикулярные хорды АВ и СД. так что, АД=3 см, а СВ=4 см. найти диаметр.есть фото во вложениях,если кому не понятно условие..
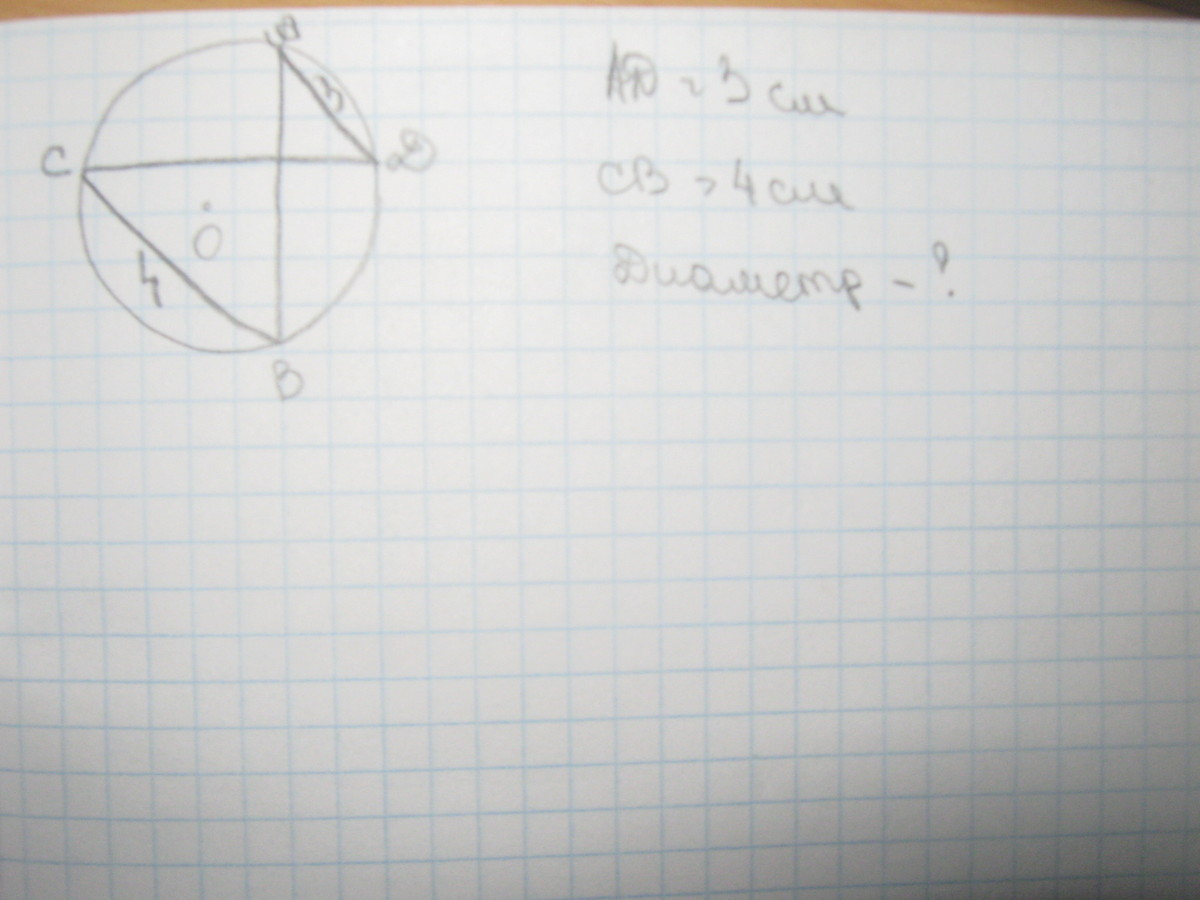
Ответы
углы BAD и BCD равны (как вписанные, опирающиеся на одну дугу BD) и
углы ADС и АBC равны (как вписанные, опирающиеся на одну дугу AC)
сумма углов BAD+ADC = BCD+ABC = 90 градусов (т.к. хорды перпендикулярны) =>
сумма соотв.дуг, на кот.опираются эти углы дуга(BD)+дуга(АС) = 180 градусов =>
оставшиеся две дуги дуга(BC)+дуга(AD) = 180 градусов ---вторая половина окружности...
на эти дуги опираются центральные углы COB и AOD => COB+AOD = 180 градусов
из треугольников COB и AOD по т.косинусов можно записать:
16 = 2r^2 - 2r^2*cos(COB)
9 = 2r^2 - 2r^2*cos(AOD) = 2r^2 - 2r^2*cos(180-COB) = 2r^2 + 2r^2*cos(COB)
система из двух уравнений...
из первого: 2r^2*cos(COB) = 2r^2 - 16
подставим во второе: 9 = 2r^2 + 2r^2 - 16
4r^2 = 25
r^2 = 25/4
r = 5/2
диаметр = 5
Если хорды АВ и СД равны, то
АВ перпендикулярна CD, то AD И СВ параллельны. ADBC трапеция вписанная в окружность, диагонали которой перпендикулярны.
Высота данной трапеции равна полусумме оснований (3+4) : 2= 3,5.
a -боковая сторона
b, с - основания
d - диагональ
по т Пифагора найдем боковую сторону =√12,5 (0,5²+3,5²=0,25+12,25=12,5)
диагональ=5 (3,5²+3,5²=12,25+12,25=25)
Диаметр=2*R=2*2.5=5