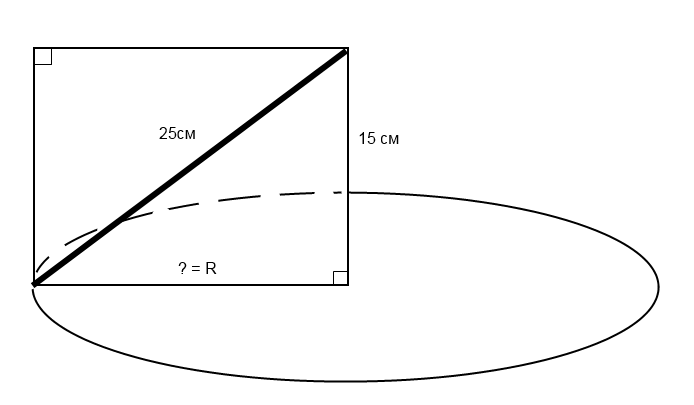
цилиндр получен вращением прямоугольника со стороной 15 м и диагональю 25 м вокруг данной стороны. найдите площадь основания цилиндра. Желательно рисунок!

Рассмотрим вначале прямоугольник. диагональ делит его на два прямоугольных треугольника со стороной в 15 м и общей стороной в 25 м. по теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, а, значит, длина стороны, которая является радиусом круга, может быть легко вычислена: , значит, , x = 20 м.

А искомая площадь основания цилиндра, то есть, площадь круга, вычисляется по формуле , где R = 20м.

Взяв , вычислим м.