Народ, помогите!

 

Концы некоторого диаметра окружности удалены от касательной, проведенной к этой окружности на 12 и 22 см. Найдите длину диаметра.


Кінці деякого діаметра кола віддалені від дотичної, проведеної до цього кола на 12 і 22 см. Знайдіть довжину діаметра.

 

Help me!!! 

Минимальное расстояние от точки до прямой - перпендикуляр.

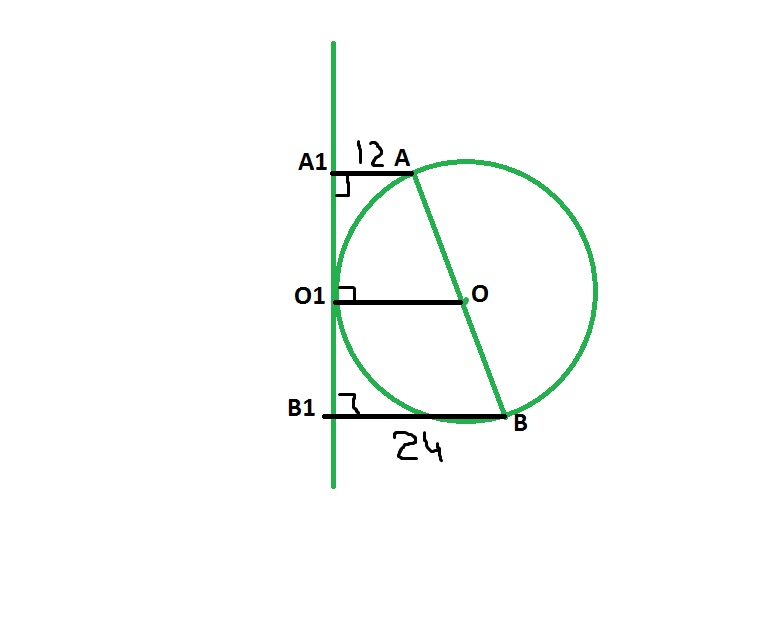
Из концов диаметра опускаем перпендикуляры на касательную.

Получаем прямоугольную трапецию с основаниями 22 и 12 см.

Большая боковая сторона трапеции равна двум радиусам.

Т.е. цент окружности точка О делит боковую сторону пополам.

Из точки О к касательной проведем радиус. Он перпендикулярен касательной, а значит параллелен основаниям трапеции.

Получается, что это средняя линия трапеции. Она равна (22+12):2 = 17 см.

А это радиус окружности.   А диаметр равен 17*2 = 34 см.

А1А перпендикулярна касательной

В1В перпендикулярна касательной

О1О перпендикулярна касательной

А1А || B1B || O1O

AO=O1O=BO=радиус

А1О=В1О

О1О- средняя линия трапеции

(12+22) : 2= 17 радиус

17*2=34 см диаметр