Предмет: Геометрия
Автор: Дилярчик
Вопрос задан 10 лет назад

< >

Найдите площадь фигуры, ограниченной линиями $y=sqrt{x}, x=1, x=4.$

Ответы

Ответ дал: konrad509

0

$\int limits_1^4 sqrt{x}, dx=\ Big[frac{2}{3}x^{frac{3}{2}}Big]_1^4=\ frac{2}{3}(4^{frac{3}{2}}-1^{frac{3}{2}})=\ frac{2}{3}(8-1)=\ frac{2}{3}cdot7=\ frac{14}{3}=4,(6)$

Приложения:

Ответ дал: Матов

0

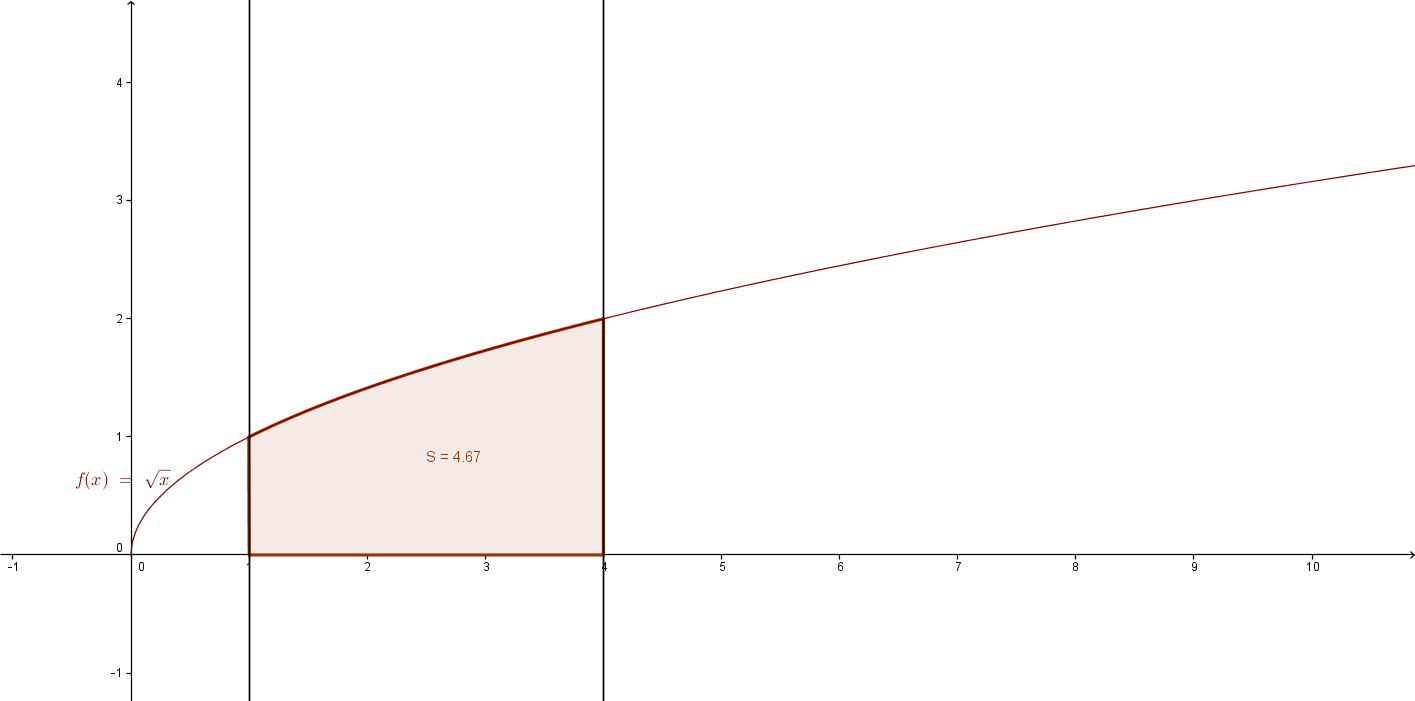
то есть нам надо интеграрировать потом находить площадь intlimits^a_b {x} , dx $intlimits^4_1 {sqrt{x}} , dx = intlimits^4_1 {frac{2sqrt{x^3}}{3}} , dx =intlimits^4_1 {frac{2sqrt{4^3}}{3}} , -frac{2sqrt{1^3}}{3}=frac{14}{3}$ единиц

Приложения:

Похожие вопросы

Английский язык

2 года назад

помогите напишите соченение на английском языке про морского котика

Русский язык

2 года назад

синонимы к словам расправил и бедняжка

Химия

7 лет назад

До складу якого числа простих речовин входять атоми Оксигену? А) 1 Б) 2 В) 3 Г) більше 3

Алгебра

7 лет назад

$x ^{2} - ( sqrt{2} + 1)x times sqrt{2} = 0 \$

История

10 лет назад

условие ништанского мирного договора(в крации) ПОМОГИТЕ ПОЖАЛУЙСТО ОЧЕНЬ НУЖНО.

Алгебра

10 лет назад

подскажите пожалуйста,как решить 2 в степени 0.5?

Математика

10 лет назад

Миша с папой посадили 7 кустов крыжовника и 18 кустов смородины. Миша посадил 6 кустов , а остальные - папа. Сколько кустов посадил папа?

География

10 лет назад

В каком направлении вы будете возвращаться домой если в магазин вы шли по азимуту 270 градусов?