АВС прямоугольный и равнобедренный, с прямым углом С, гипотенуза АВ = 4 см. Отрезок СМ перпендикулярен плоскости треугольника и равен 2 см. найдите расстояние от точки М до АВ

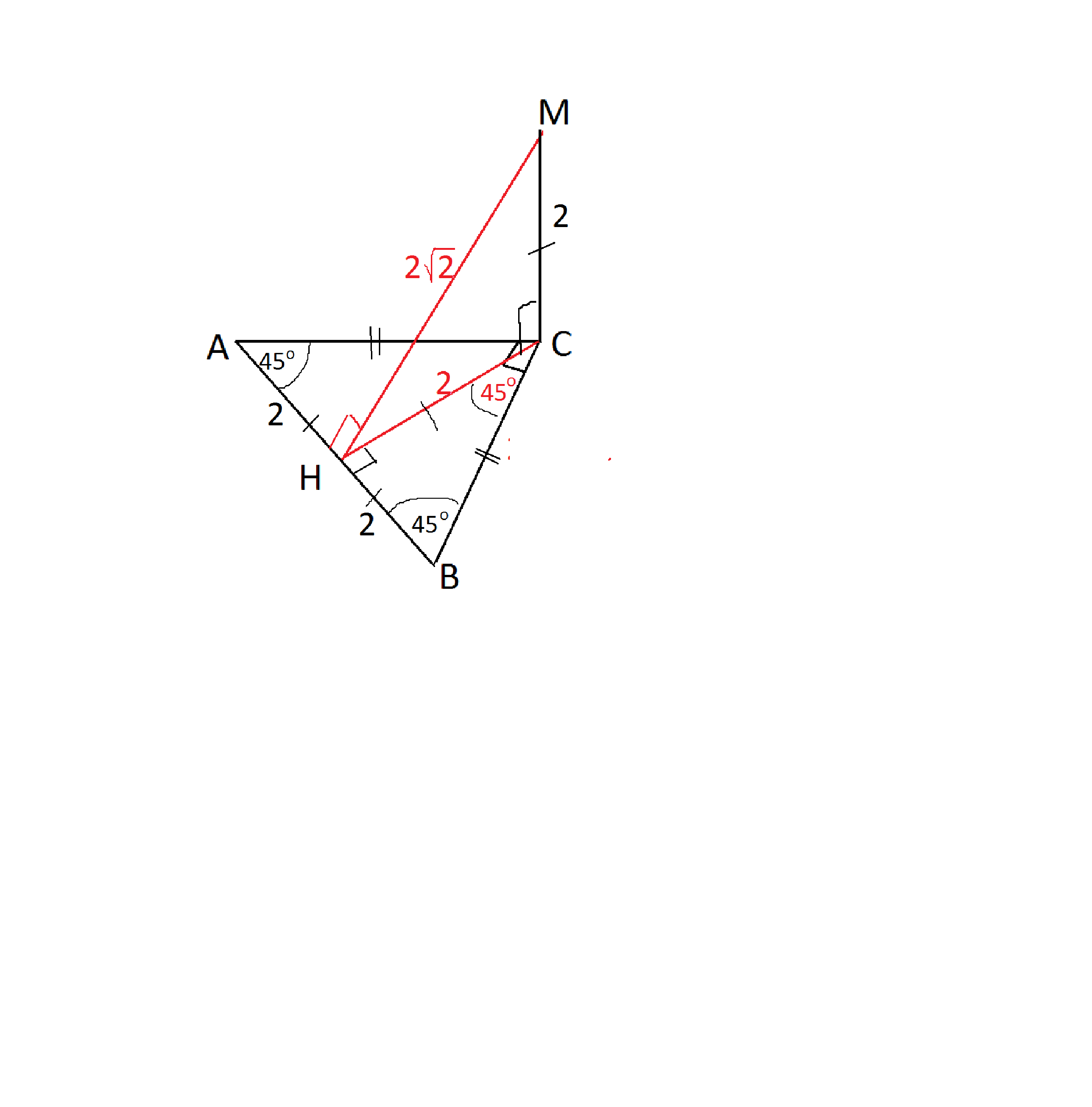
Треугольник АВС прямоугольный, равнобедренный.

СН в нем - высота, биссектриса и медиана, и делит его

на два равнобедренных

прямоугольных треугольника с катетами, равными половине гипотенузы. 

Эта же высота является проекцией наклонной МН, перпендикулярной к АВ, - расстояния от М до АВ ( по т. о трех перпендикулярах)

Треугольник НСМ - прямоугольный по условию.

МС и НС - катеты.

По теореме Пифагора

МН²=МС²+НС²=8
МН= 2√2 см