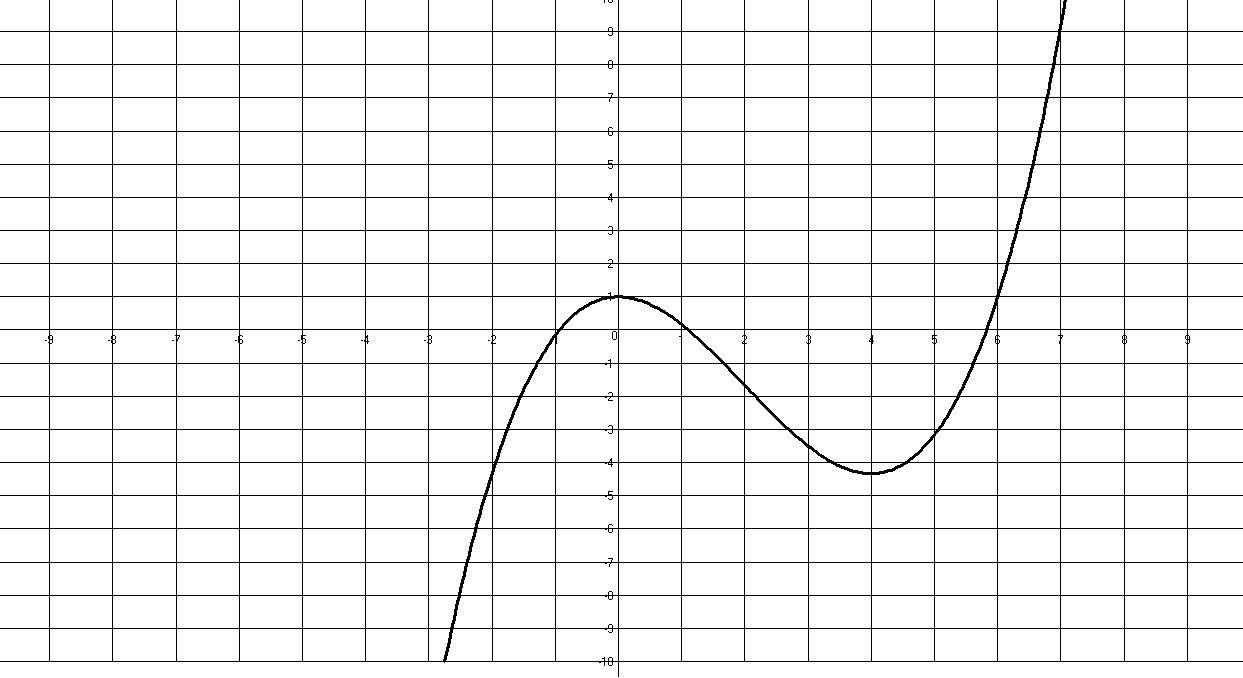
Дослідити функцію методами диференціального числення та використовуючи результати досджень,побудувати її графік
помогите срочно надо
Ответы
οбласть :
первая производная :
второя производная :
принципя
1. f(x) возрастающая если производная > 0
2. f(x) убывающая если производная < 0
3. f(x) неубывающая и невозрастающая (стала или екстремум ) если производная = 0
4. f(x) вypuкла если второя производная > 0
5. f(x) вогнутая если второя производная < 0
6. f(x) невypuкла и невогнутая ( перегиб или прямая ) если второя производная = 0
ад 3
екстрема
ад 1
возрастание
ад 2
убывание
</var></var></p>
<p> </p>
<p> </p>
<p>ad 6</p>
<p> </p>
<p>перегиб</p>
<p> </p>
<p><img src=[/tex]x-2 =0 newline newline x=2" title="0<x<4" title="x-2 =0 newline newline x=2" title="0<x<4" alt="x-2 =0 newline newline x=2" title="0<x<4" />
ad 6
перегиб
ad 6
перегиб
ad 4
выпукла:
ад 5
вогнутая
тепер рисуем : во вложению граф
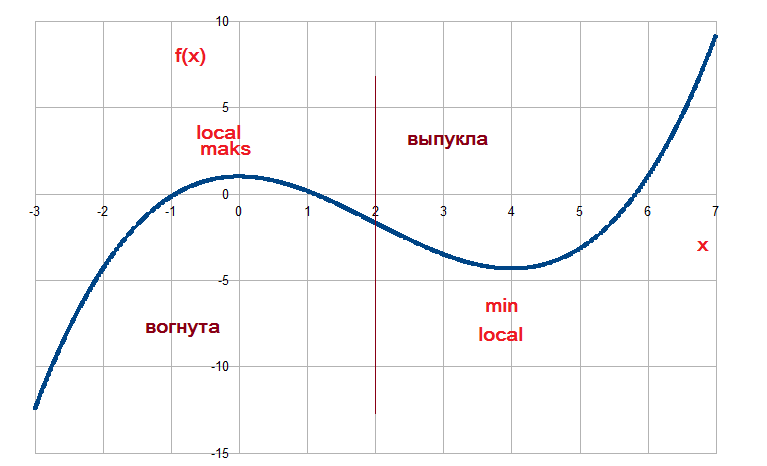
y'=0.5x²-2x
0.5x²-2x=0
x(0.5x-2)=0
x=0 или 0.5x-2=0
0.5x=2
x=4
-----+--------0------------4-------+------>
(-∞;0)∨(4;∞) возрастает
(0;4) убывает
х=0 точка max (0;1)
х=4 точка min (4; -4,3333)