Высота прямоугольного треугольника делит гипотенузу на отрезки 12.6см и 22.4 см. Найдите длины отрезков гипотенузы, на которые её делит биссектриса прямого угла

Ответы

Ответ дал: artalex74

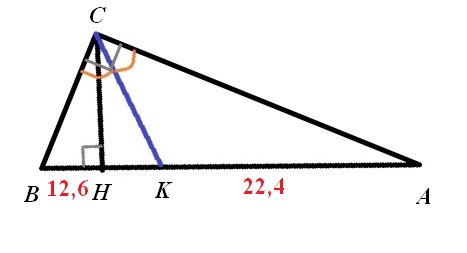
Чертеж к задаче во вложении.

Пусть СН - высота, СК - биссектриса.

По свойству пропорциональных отрезков в прямоугольном треугольнике:

$AC=sqrt{AH*AB}=sqrt{22.4*35}=28 \ BC=sqrt{BH*AB}=sqrt{12.6*35}=21$

По свойству биссектрисы угла треугольника:

$frac{AK}{AC}=frac{BK}{BC}, \ AB=BH+AH=12,6+22,4=35 \ BK=35-AK \ frac{AK}{28}=frac{35-AK}{21} \ frac{AK}{4}=frac{35-AK}{3} \ 3AK=140-4AK \ 7AK=140 \ AK=20 \ BK=35-20=15$

Ответ: 15 см и 20 см.

Приложения:

Похожие вопросы

Русский язык

2 года назад

какая часьть речи у слова наползла

Русский язык

2 года назад

Образуйте от полных форм причастий и прилагательных краткие формы. Образец: склонённая голова - голова склонена (прич.) болезненные воспоминания- воспоминания болезненны

Математика

7 лет назад

Номер 457, нечетные надо решить!

Литература

7 лет назад

Кто из перечисленных авторов был поэтом Бианки Андерсен Паустовский или Тютчев

Математика

10 лет назад

В 8 часов расстояние между 2катерами, плывущими навстречу друг другу, было 250 км .скорости катеров 25км/ч и 35 км/ч .Встретяться ли они до 12 часов того же дня?Через сколько времени произойдёт

Химия

10 лет назад

Рассчитайте сколько граммов фосфата кальция образуется при реакции нейтрализации гидроксида кальция массой 7,4 г

Алгебра

10 лет назад

. Пароход проходит против течения реки путь от Астрахани до Казани за 6 суток, а от Казани до Астрахани, по течению, за 4 суток. За сколько суток пройдёт то же расстояние плот?

Алгебра

10 лет назад

Пол в комнате прямоугольной формы размером 20× 15 м нужно покрыть квадратными плитками со стороной 20 см. Сколько потребуется плиток?