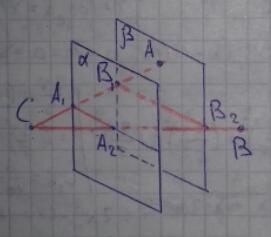
Плоскость альфа пересекает стороны угла ACB в точках A1 и А2, а параллельная ей плоскость бета - в точках B1 и B2. Найдите B1B2, если CB1=14 дм, СА1:А1B1=2:5, а A1A2=A1B1

A₁A₂║B₁B₂ как линии пересечения параллельных плоскостей α, β и плоскости (ACB), поэтому ΔA₁CA₂ ~ ΔB₁CB₂

Пусть CA₁ = 2x, тогда A₁B₁ = 5x.

CA₁+A₁B₁ = CB₁

2x+5x = 14дм = 7x ⇒ x = 2дм.

A₁B₁ = 5·2 = 10дм

A₁A₂ = A₁B₁ = 10дм

Из подобия треугольников A₁CA₂ и B₁CB₂ следует:

B₁B₂ : A₁A₂ = CB₁ : CA₁ = 7x : 2x = 3,5

B₁B₂ = 3,5·A₁A₂ = 3,5·10 = 35дм

Ответ: 35дм.