Найти радиус окружности, описанной около равнобедренного треугольника с основанием 16 см и высотой 4 см.

Формула радиуса окружности, описанной около треугольника:
R=a•b•c:4S, где a,b,c – стороны треугольника, S - его площадь.
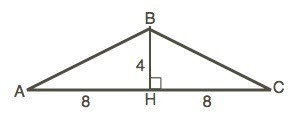
Пусть в ∆ АВС АВ=ВС, ВН - высота и медиана равнобедренного треугольника. 
Тогда ∆ АВН - прямоугольный. По т.Пифагора 
АВ=BC=√(AH²+BH²)=√(64+16)=4√5 см
S=ВН•AC:2=32 см²