Решите 5 задание ..................

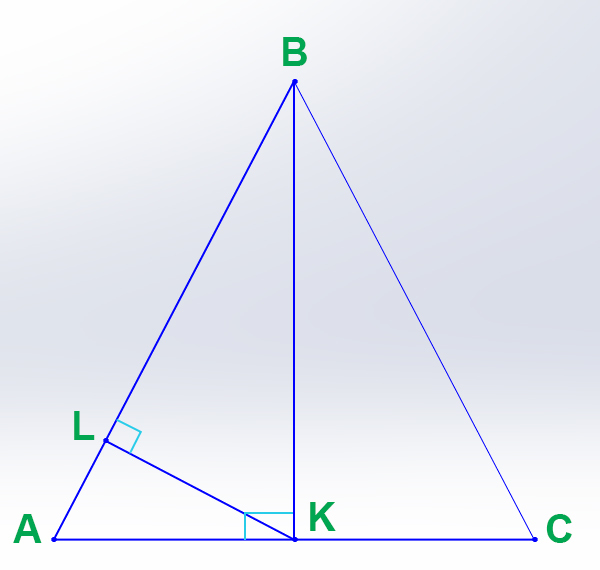
Рассечем конус вертикальным сечением, получим вид см. прикрепленный рисунок (BK - высота конуса, AB -образующая, AK - радиус основания конуса).

ΔABK~ΔBLK (признак подобия треугольников по двум углам - ∠AKB=∠BLK и ∠ABK=∠KBL), из этого можно записать

⇒

По теореме Пифагора BL²=BK²-KL²=(4√3)²-(2√3)²=36 ⇒ BL=6 см

см

По теореме Пифагора найдем  AK:

AK²=AB²-BK²=(8)²-(4√3)²=16 ⇒ AK=√16=4 см

Площадь боковой поверхности конуса равна:

S=π*AK*AB=π*4*8=32π см²