Найти наименьшее расстояние между машинами, движущимися со скоростями 16 мс и 36кмч по дорогам, пересекающимися под углом 60, если в тот момент когда расстояние между машинами было равно 1.4км, соединяющая их прямая была перпендикулярна одной из дорог

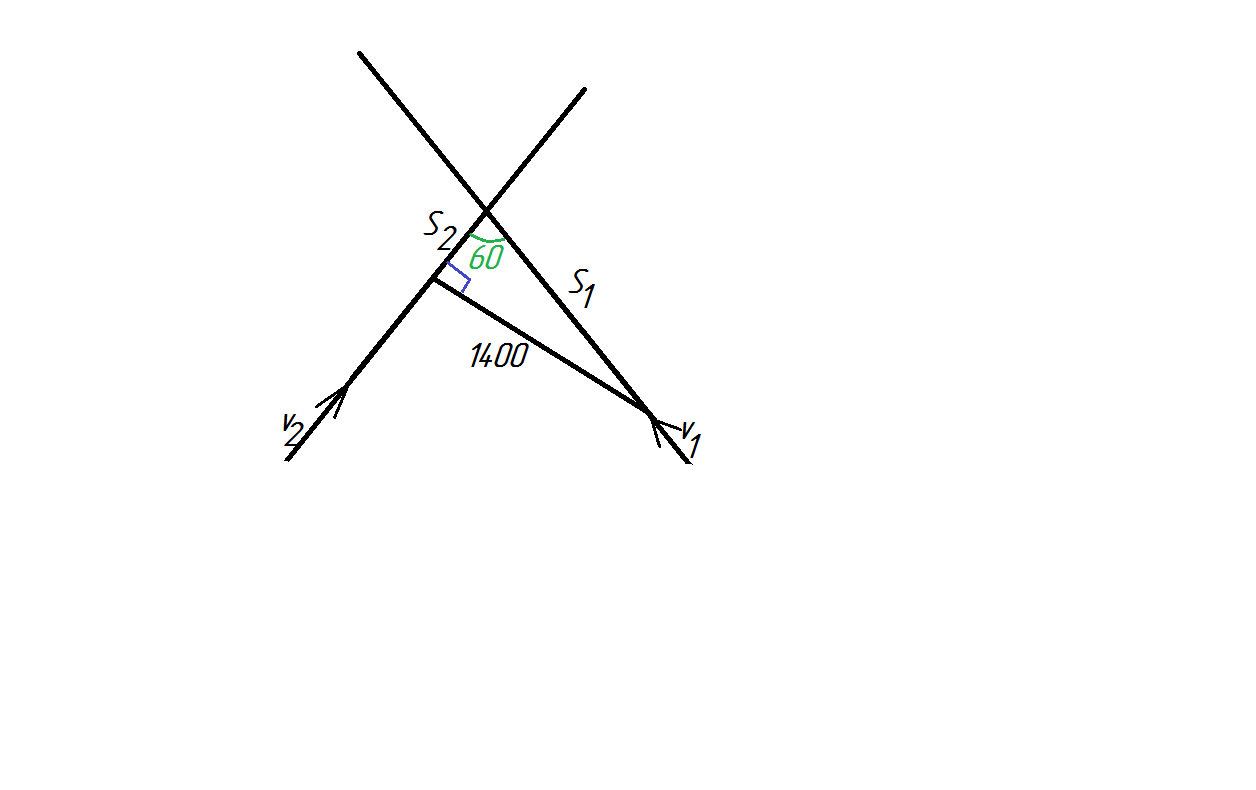
На рисунке показана линия соединяющая автомобили, исходя из отношений в прямоугольном треугольнике, находим длины оставшихся отрезков, до точки пресечения:



Расстояние будет наименьшим когда второй автомобиль проедет оставшееся расстояние, найдем время за которое он проедет это расстояние:

Теперь найдем расстояние которое пройдет первый автомобиль за это же время:

Тогда наименьшее расстояние будет равно:
м
Ответ: 1264 метра