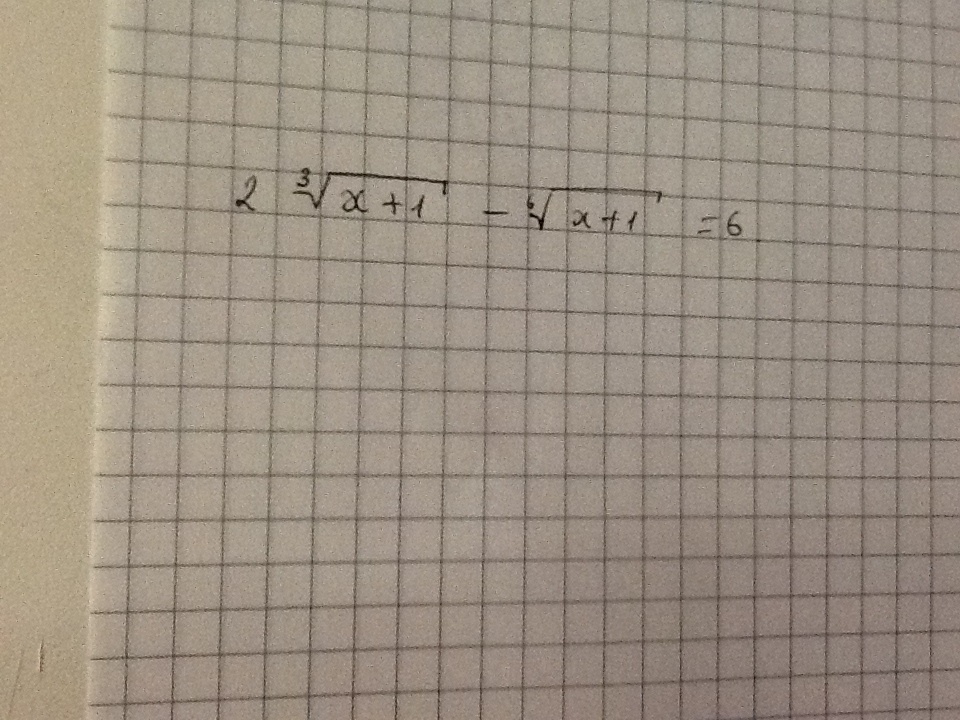Ответы
Ответ дал:
0
Обозначим корень шестой степени через t.
![sqrt[6]{x+1}=t >0to sqrt[3]{x+1}=t^2\2t^2-t-6=0\D=1+8cdot 6=49, sqrtD=7\t_1=frac{1-7}{4}=-frac{6}{4}=-frac{3}{2}<0\t_2=2>0\sqrt[6]{x+1}=2\x+1=2^6\x+1=64\x=63](https://tex.z-dn.net/?f=sqrt%5B6%5D%7Bx%2B1%7D%3Dt+%26gt%3B0to+sqrt%5B3%5D%7Bx%2B1%7D%3Dt%5E2%5C2t%5E2-t-6%3D0%5CD%3D1%2B8cdot+6%3D49%2C+sqrtD%3D7%5Ct_1%3Dfrac%7B1-7%7D%7B4%7D%3D-frac%7B6%7D%7B4%7D%3D-frac%7B3%7D%7B2%7D%26lt%3B0%5Ct_2%3D2%26gt%3B0%5Csqrt%5B6%5D%7Bx%2B1%7D%3D2%5Cx%2B1%3D2%5E6%5Cx%2B1%3D64%5Cx%3D63 "sqrt[6]{x+1}=t >0to sqrt[3]{x+1}=t^2\2t^2-t-6=0\D=1+8cdot 6=49, sqrtD=7\t_1=frac{1-7}{4}=-frac{6}{4}=-frac{3}{2}<0\t_2=2>0\sqrt[6]{x+1}=2\x+1=2^6\x+1=64\x=63")
При решении примера чли, что корни чётных степеней могут быть только положительными, отрицательное значение не подходит.
При решении примера чли, что корни чётных степеней могут быть только положительными, отрицательное значение не подходит.
Похожие вопросы
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад