помогите решить, не срочно, очень нужно. ВООБЩЕ НЕ ПОНИМАЮ
решить задачу Коши для ОДУ первого порядка...
Проинтегрировать однородное ОДУ
Приложения:
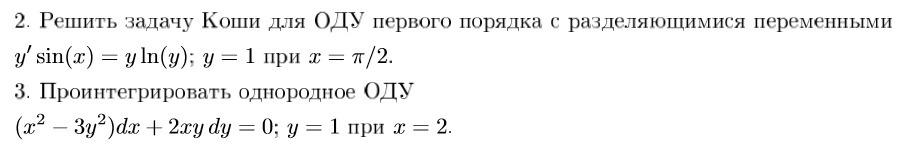
Ответы
Ответ дал:
0
2) С разделяющимися переменными - совсем просто.
dy/dx*sin x = y*ln(y)
Разделяем переменные
dy/(y*ln(y)) = dx/sin x
Интегрируем обе части.



Получаем

Избавляемся от внешних логарифмов

y = e^(C*tg(x/2))
Это правильно, я проверил на сайте Вольфрам Альфа
Теперь решаем задачу Коши
y(pi/2) = 1
e^(C*tg(pi/4)) = e^(C*1) = e^C = 1
C = 0
Но тогда получается
y = e^0 = 1, чего не может быть.
Вывод: Такие условия в задаче Коши не могут быть.
3) (x^2 - 3y^2) dx + 2xy dy = 0; y(2) = 1
Перепишем так:
(x^2 - 3y^2) + 2xy*dy/dx = 0
(x^2 - 3y^2) + 2xy*y' = 0
Это однородное уравнение 1 порядка, решается заменой
y(x) = x*t(x), тогда y'(x) = t(x) + x*t'(x)
x^2 - 3x^2*t^2 + 2x*x*t*(t + x*t') = 0
Делим все на x^2
1 - 3t^2 + 2t^2 + 2tx*t' = 0
1 - t^2 + 2tx*t' = 0
Получили уравнение с разделяющимися переменными
2tx*dt/dx = t^2 - 1
2t/(t^2 - 1) dt = dx/x
Замена t^2 - 1 = z, тогда dz = 2t dt
dz/z = dx/x
z = t^2 - 1 = x + C
t(x) = √(x+1+C)
Мы заменяем C + 1 на C1, потому что это все равно константа.
y(x) = x*t(x) = x*√(x+C+1)
Теперь решаем задачу Коши
y(2) = 2*√(2 + C + 1) = 2√(C + 3) = 1
C + 3 = (1/2)^2 = 1/4
C = -3 + 1/4 = -3 + 0.25 = -2,75
Ответ: y(x) = x*√(x-1,75)
dy/dx*sin x = y*ln(y)
Разделяем переменные
dy/(y*ln(y)) = dx/sin x
Интегрируем обе части.
Получаем
Избавляемся от внешних логарифмов
y = e^(C*tg(x/2))
Это правильно, я проверил на сайте Вольфрам Альфа
Теперь решаем задачу Коши
y(pi/2) = 1
e^(C*tg(pi/4)) = e^(C*1) = e^C = 1
C = 0
Но тогда получается
y = e^0 = 1, чего не может быть.
Вывод: Такие условия в задаче Коши не могут быть.
3) (x^2 - 3y^2) dx + 2xy dy = 0; y(2) = 1
Перепишем так:
(x^2 - 3y^2) + 2xy*dy/dx = 0
(x^2 - 3y^2) + 2xy*y' = 0
Это однородное уравнение 1 порядка, решается заменой
y(x) = x*t(x), тогда y'(x) = t(x) + x*t'(x)
x^2 - 3x^2*t^2 + 2x*x*t*(t + x*t') = 0
Делим все на x^2
1 - 3t^2 + 2t^2 + 2tx*t' = 0
1 - t^2 + 2tx*t' = 0
Получили уравнение с разделяющимися переменными
2tx*dt/dx = t^2 - 1
2t/(t^2 - 1) dt = dx/x
Замена t^2 - 1 = z, тогда dz = 2t dt
dz/z = dx/x
z = t^2 - 1 = x + C
t(x) = √(x+1+C)
Мы заменяем C + 1 на C1, потому что это все равно константа.
y(x) = x*t(x) = x*√(x+C+1)
Теперь решаем задачу Коши
y(2) = 2*√(2 + C + 1) = 2√(C + 3) = 1
C + 3 = (1/2)^2 = 1/4
C = -3 + 1/4 = -3 + 0.25 = -2,75
Ответ: y(x) = x*√(x-1,75)
Похожие вопросы
2 года назад
2 года назад
6 лет назад
6 лет назад
9 лет назад