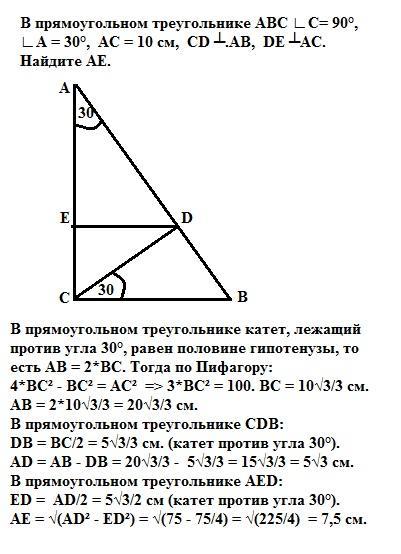
В прямоугольном треугольнике ABC ∟С= 90°,∟.A = 30°, АС = 10 см, CD ┴.АВ, DE ┴АС.
Найдите АЕ.
а) 8 см; б) 6 см; в) 5 см; г) 7,5 см.

Ответ:

г) 7,5 см.

Объяснение:

В прямоугольном треугольнике катет, лежащий против угла 30°, равен половине гипотенузы, то есть АВ = 2*ВС. Тогда по Пифагору:

4*ВС² - ВС² = АС²  => 3*ВС² = 100. ВС = 10√3/3 см.

AB = 2*10√3/3 = 20√3/3 см.

В прямоугольном треугольнике CDB:

DB = BC/2 = 5√3/3 см. (катет против угла 30°).

AD = AB - DB = 20√3/3 -  5√3/3 = 15√3/3 = 5√3 см.

В прямоугольном треугольнике AED:

ED =  AD/2 = 5√3/2 см (катет против угла 30°). Тогда по Пифагору:

AE = √(AD² - ED²) = √(75 - 75/4) = √(225/4)  = 7,5 см.