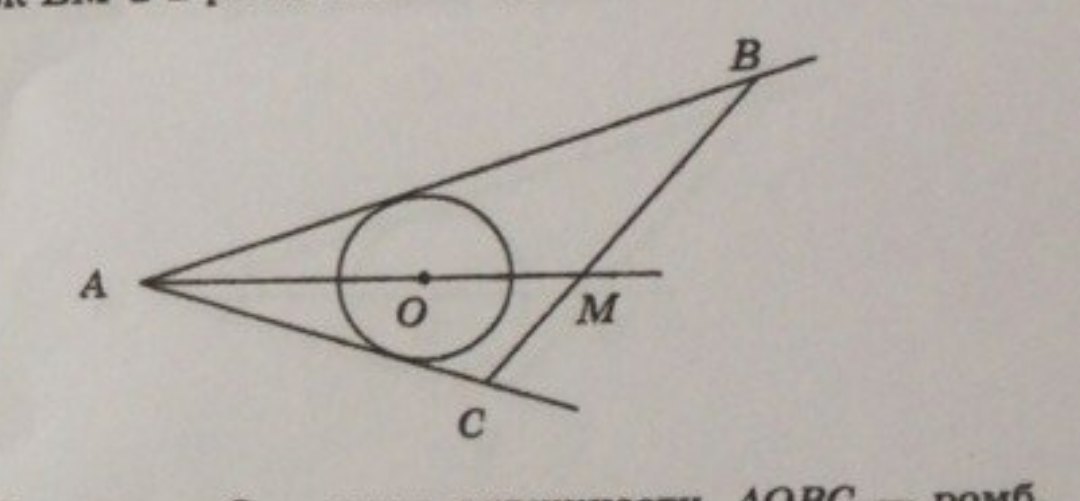
на рисунке ав и ас касательные к окружности с центром о. найдите длину отрезка ав, если ас - 24 см, а отрезок вм в 2 раза больше отрезка см
Ответы
Ответ дал:
0
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центрокружности ⇒ AM - биссектриса угла CAB
Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам (свойство биссектрисы).
СМ : BM = AC : AB
BM = 2CM (по условию)
CM : 2CM = 24 : AB
CM/2CM = 24/AB
1/2 = 24/AB
Свойство пропорции - произведение крайних членов равно произведению средних
1* AB = 2*24
AB = 48 (см)
.
Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам (свойство биссектрисы).
СМ : BM = AC : AB
BM = 2CM (по условию)
CM : 2CM = 24 : AB
CM/2CM = 24/AB
1/2 = 24/AB
Свойство пропорции - произведение крайних членов равно произведению средних
1* AB = 2*24
AB = 48 (см)
.
Приложения:
Похожие вопросы
2 года назад
2 года назад
6 лет назад
6 лет назад
9 лет назад
9 лет назад
9 лет назад
9 лет назад