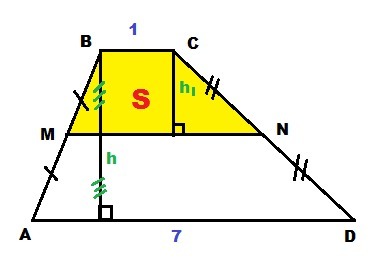
В трапеции ABCD известно, что AD = 7, BC = 1, а её площадь равна 64. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD

Средняя линия трапеции  NM = 

Из площади трапеции можно найти высоту трапеции


Средняя линия NM  трапеции ABCD делит высоту h пополам 
h₁ = h/2 = 16/2 = 8



Ответ: площадь трапеции BCNM равна 20