• Предмет: Геометрия
  • Автор: Знания
  • Вопрос задан 8 лет назад
< >

В треугольнике ABC угол C равен 90°, AC=2, sinA=(√17):17 . Найдите BC.

Ответы

Ответ дал: Hrisula
0

Из тождества sin²α+cos²α=1 

 cosA= sqrt{1- frac{17}{289} } = sqrt{ frac{17*17-17}{289} } = sqrt{ frac{17*16}{289} } = frac{4 sqrt{17} }{17}


 AB=AC:cosA= frac{2}{ frac{4 sqrt{17} }{17}} = frac{2*17}{4 sqrt{17} } = frac{ sqrt{17} }{2}


BC=AB*sinA= frac{ sqrt{17} * sqrt{17}}{2*17} = frac{1}{2}

---------------

Как вариант: 

Обозначим коэффициент этого отношения равным а. 

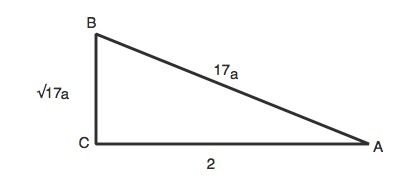
Тогда ВС=a√17,  AB=17a

По т.Пифагора 

АВ²-ВС²=АС²

17•17a²-17a²=4

17a²•(17-1)=4

a²=4:17•16 =1:17•4

a²=17:(17•17•4) 

a=√17:(17•2)

BC= frac{ sqrt{17}* sqrt{17}}{17*2}= frac{1}{2}

Приложения:
Похожие вопросы
Русский язык
2 года назад
прочитайте.укажите предложения,грамматическая основа которых состоит из одного главного члена Светает.Тишина.Подул свежий ветерок.Скоро запоют в роще птицы.
Русский язык
2 года назад
Прочитай текст. Выпиши предложения, в которых допущены ошибки. Обозначь окончания существительных и прилагательных. Живое пламя. Издали маки похожи на зажжённые факелы с живыми, весело полыхающими
Экономика
6 лет назад
Пожалуйста, помогите написать эссе на тему «Трансформация криптовалютного рынка в мире в 2022 г.»
Литература
6 лет назад
Составь 5 вопросов на текст Загадка пустой планеты ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО
Алгебра
9 лет назад
найдите уравнение прямой,проходящей через точку с координатами (1;3), касающейся графика функции y=8 корень из X - 7 и пересекающей в двух различных точках график функции y=x^2+4x-1
Математика
9 лет назад
Помогите с номером 5 пожалуйста!!!!
Математика
9 лет назад
(8 в квадрате * 6 + 4928) кг = кг (3 в кубе * 10 * 1000 – 230 000 ) кг = кг 9 в квадрате км – (35 200 м * 2) = м
Физика
9 лет назад
тело отчёта чтооо это такаееееее