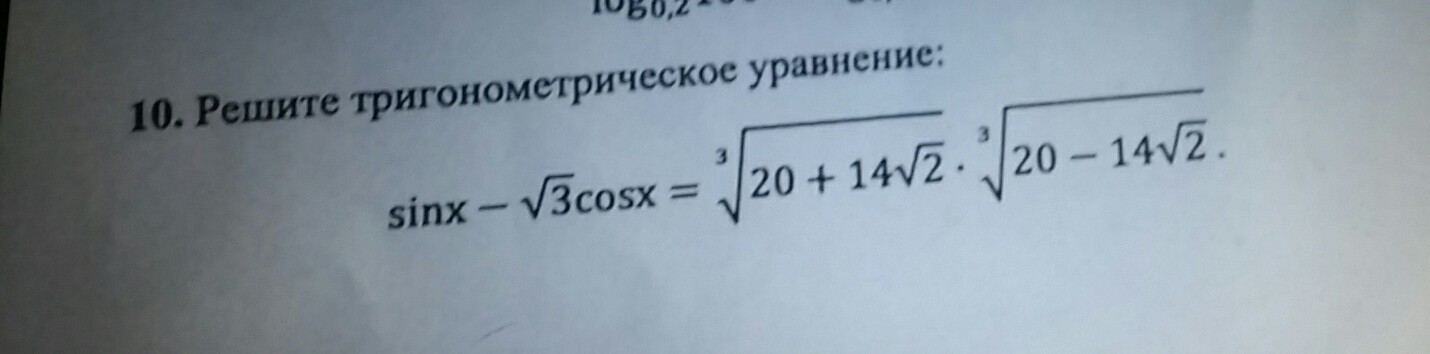Ответы
Ответ дал:
0
sinx-√3cosx=![sqrt[3]{20+14 sqrt{2} }* sqrt[3]{20-4 sqrt{2} }](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B20%2B14+sqrt%7B2%7D+%7D%2A+sqrt%5B3%5D%7B20-4+sqrt%7B2%7D+%7D+ "sqrt[3]{20+14 sqrt{2} }* sqrt[3]{20-4 sqrt{2} }")
sinx-√3cosx=![sqrt[3]{(20^2-14^2*2}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B%2820%5E2-14%5E2%2A2%7D+ "sqrt[3]{(20^2-14^2*2}")
sinx-√3cosx=![sqrt[3]{20^2-14^2*2}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B20%5E2-14%5E2%2A2%7D+ "sqrt[3]{20^2-14^2*2}")
sinx-√3cosx=![sqrt[3]{8}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B8%7D+ "sqrt[3]{8}")
sinx-√3cosx=2
1/2*sinx-√3/2*cosx=1
1/2=sin(pi/6)
√3/2=cos(pi/6)
sinx*sin(pi/6)-cosx*cos(pi/6)=1
cosx*cos(pi/6)-sinx*sin(pi/6)=-1
cos(x+pi/6)=-1
x+pi/6=pi+2pi*n n∈Z
x=5pi/6+2pi*n n∈Z
sinx-√3cosx=
sinx-√3cosx=
sinx-√3cosx=
sinx-√3cosx=2
1/2*sinx-√3/2*cosx=1
1/2=sin(pi/6)
√3/2=cos(pi/6)
sinx*sin(pi/6)-cosx*cos(pi/6)=1
cosx*cos(pi/6)-sinx*sin(pi/6)=-1
cos(x+pi/6)=-1
x+pi/6=pi+2pi*n n∈Z
x=5pi/6+2pi*n n∈Z
Ответ дал:
0
метод ввода дополнительного аргумента
Похожие вопросы
2 года назад
2 года назад
6 лет назад
6 лет назад
9 лет назад
9 лет назад