Зарядка для хвоста-7. Задача для супер-пупер знатоков! Придумал, но в свое время не смог решить. Вот теперь "добил" ее. Так что попробуйте и вы тоже.
Построить треугольник по стороне, радиусу описанной окружности и биссектрисе угла, противоположному этой стороне. ("биссектриса" - подразумевается что это отрезок биссектрисы от угла до стороны)
Дерзайте, авось получится!
cos20093:
Но близко :) Пусть AB - заданная хорда в нарисованной окружности с центром O (ясно, что это строится элементарно). Через середину хорды M проводится диаметр DF. D и F - середины дуг AB, это понятно. Пусть D - середина меньшей (нижней) дуги. Угол DAB как раз очень нужен для построения :) Из точки M надо провести прямую так, чтобы она образовывала этот угол с прямой DF. Потом от точки M вверх откладывается биссектриса, конец - точка K. Остается провести через К прямую II AB
Ой, не наврал ли я ? :))))
Ну не верно, разумеется, угол это не при чем
конечн, нужно... :) НУЖНО построить треугольник :) хи-хи... Так что ответы давайте в ответе.... Я ж говорил, что придумал задачу от нечего делать, и не смог решить. А тут вчера - бац по мозгам! - решение как на ладони... :)
А, ну еще проще. DM же построен, а DM*MF = DC1*C1C (C1 - основание биссектрисы). Тут по сути известно всё - СС1 задано, а отрезки диаметра DM и MF построены. Построить DC1 = DM*MF/L не трудно. Дальше очевидно.
Я для построения отрезка типа d = ab/c пользуюсь теоремой о секущей (там все прозрачно), но наверно есть и другие способы.
и почему ж DM*MF = DC1*C1C (C1 - основание биссектрисы).? А?
:( блин, надо прекращать сидеть тут на работе :((((
А все равно работает :) идея то была правильная. DM/DC1 = DC/DF; обозначу DM = d; DC1 = x; C1C = L; d/x = (x + L)/2R; x(L+x) = 2Rd; вот тут уже все верно. Такое уравнение геометрически решается с помощью вспомогательной окружности, построенной как на диаметре на отрезке 2R - d
что-то я вас не пойму. если имеете что сказать - рисуйте, не стесняйтесь... Из ваших рассуждений не понятно, где точка С, где С1, и что такое L. Так что - ответ с рисунком - в студию. Иначе - все, что вы сказали - неправильно
Ответы
Ответ дал:
3
Так, вторая попытка :) Постараюсь коротко.
1) Окружность заданного радиуса R.
2) в ней хорда заданной длины AB.
3) диаметр DF через середину AB - точку M; обозначу DM = d;
4) на MF, как на диаметре, строится окружность. O1 - её центр
5) DK - касательная к этой окружности, её длина в квадрате равна 2R*d
6) продлить O1K на половину заданной длины биссектрисы L/2; тогда
DP^2 = (L/2)^2 + 2Rd;
7) продлить DP на L/2; до точки C2;
8) полученным радиусом DC2 провести окружность с центром в D до пересечения с первой окружностью. Это точка C - третья вершина треугольника ABC.
Смысл построения вот в чем. Где бы не лежала точка С на окружности, биссектриса угла С все равно придет в точку D. Пусть при этом она пересекает AB в точке C1. По условию CC1 = L - заданная величина.
Очевидно, что DM/DC1 = DC/DF; или, если обозначить DC1 = x; то
d/x = (x + L)/(2R); или x^2 + x*L - 2Rd = 0; (x + L/2)^2 = (L/2)^2 + 2Rd; (это я просто решил квадратное уравнение :))
Отрезок DP на чертеже как раз и построен так, что DP^2 = (L/2)^2 + 2Rd;
1) Окружность заданного радиуса R.
2) в ней хорда заданной длины AB.
3) диаметр DF через середину AB - точку M; обозначу DM = d;
4) на MF, как на диаметре, строится окружность. O1 - её центр
5) DK - касательная к этой окружности, её длина в квадрате равна 2R*d
6) продлить O1K на половину заданной длины биссектрисы L/2; тогда
DP^2 = (L/2)^2 + 2Rd;
7) продлить DP на L/2; до точки C2;
8) полученным радиусом DC2 провести окружность с центром в D до пересечения с первой окружностью. Это точка C - третья вершина треугольника ABC.
Смысл построения вот в чем. Где бы не лежала точка С на окружности, биссектриса угла С все равно придет в точку D. Пусть при этом она пересекает AB в точке C1. По условию CC1 = L - заданная величина.
Очевидно, что DM/DC1 = DC/DF; или, если обозначить DC1 = x; то
d/x = (x + L)/(2R); или x^2 + x*L - 2Rd = 0; (x + L/2)^2 = (L/2)^2 + 2Rd; (это я просто решил квадратное уравнение :))
Отрезок DP на чертеже как раз и построен так, что DP^2 = (L/2)^2 + 2Rd;
Приложения:
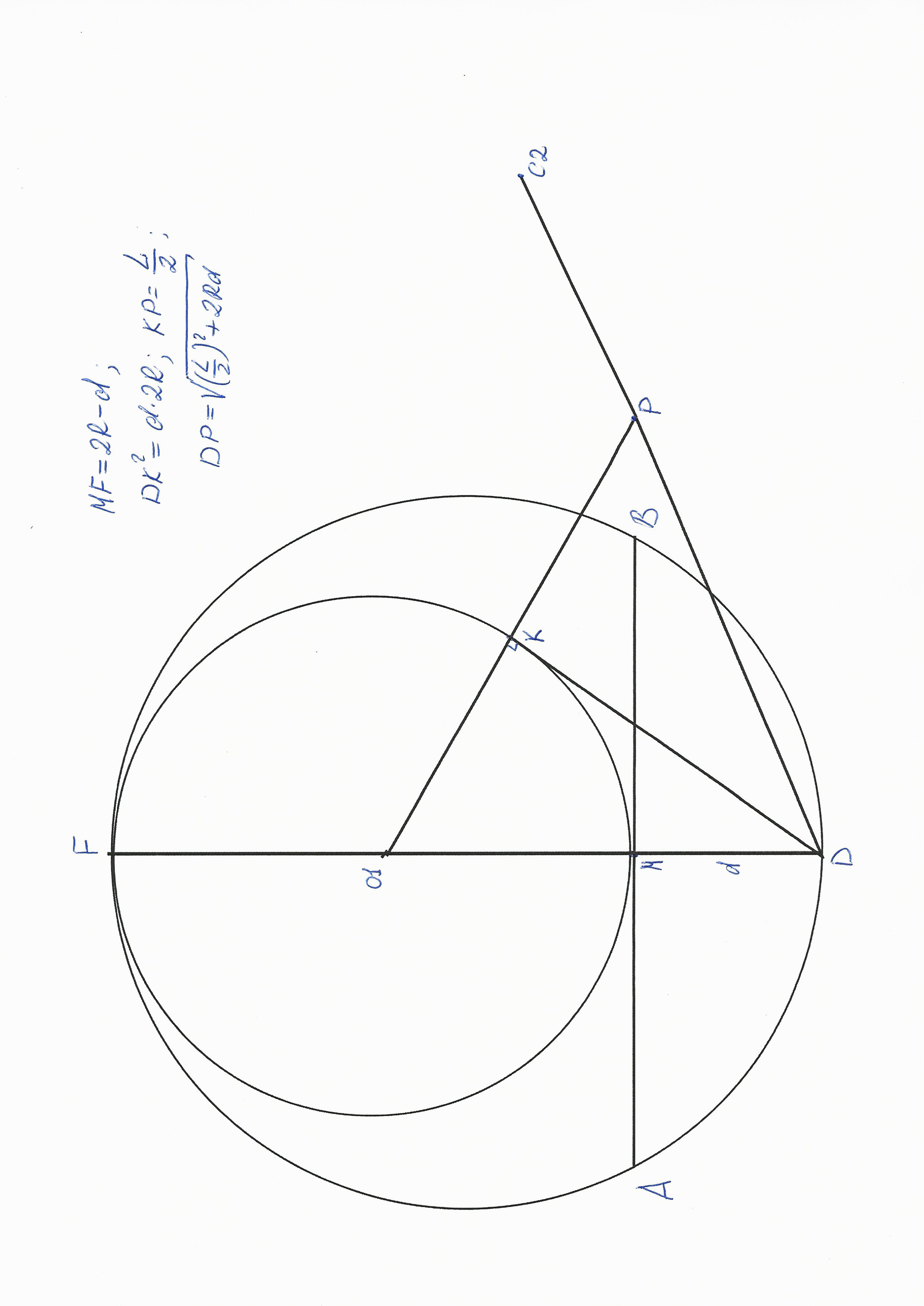
не правильно, я сейчас сделаю правильно, там не та окружность
та понятно, что не та, вы ж указали, да и мне ясно, что к чему и как. Принцип ясен.Так же и я решал. А второе решение у меня без доп. окружности.. Правда , модеры могут зарезать, что не так.
Выложил построение, а обоснование выпало в результате, ну не страшно. Я сейчас добавлю его.
Ну вот, вроде всё :) Я убрал пояснения, как строить касательную из точки D - это вообще делается одной линейкой, да и не я это придумал, конечно :) Вообще туповатое решение, но результат дает. Я уверен, что есть решение на много проще и красивее.
есть такой сайт http://geometry.ru/ а там есть ссылка еще на один сайт - "Задачи-головоломки по геометрии". Я всем очень рекомендую.
Для модераторов - на всякий случай, а то мало-ли какой попадется... Это образовательные сайты, а не альтернативные сервисы. Интересны они только для достаточно продвинутых - для повышения образовательного уровня. Так что я тут не занимаюсь "рекламой конкурентов", а наоборот - рекомендую ресурсы, косвенно способствующие повышению качества ответов. Это то же самое, как рекомендовать учебник. (Интересно, что я услышу в ответ :) жаль, поспорить не с кем.)
в ответ могу сказать только - 1) я на пояснения даже не смотрел, все понятно из рисунка, даже на прошлом рисунке ( ну не тот диаметр случайно взял :) с кем не бывает) все сразу понятно.. Еще одну задачку придумал, но мне сказали , что она нерешаемая (сам не могу к ней подступиться)
а по поводу сайта- зашел, глянул скриншоты видео - не, для меня слишком сложно.....
сайт ладно, а вторую ссылку посмотрите :)
вот еще одно мое решение - https://znanija.com/task/24858510
Ответ дал:
3
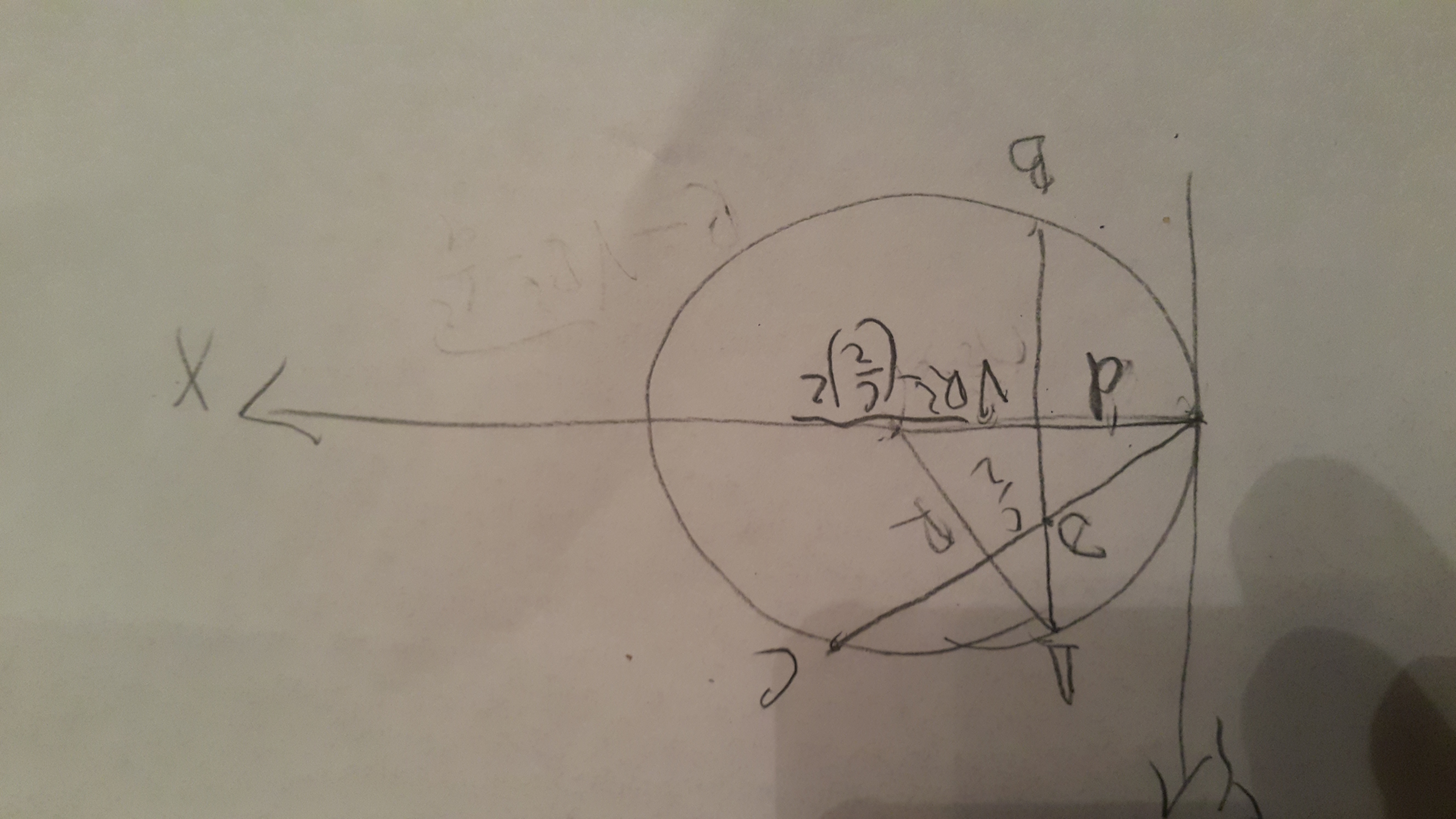
Описанная окружность  (центр расположили на оси OX); в полярных координатах
(центр расположили на оси OX); в полярных координатах  Прямая x=d пересекает окружность в точках A и B (|AB|=c известно,
Прямая x=d пересекает окружность в точках A и B (|AB|=c известно,  ). Луч, выходящий из начала координат и образующий угол
). Луч, выходящий из начала координат и образующий угол
 с осью OX, пересекает AB в точке D:
с осью OX, пересекает AB в точке D:  а окружность пересекает в точке C :
а окружность пересекает в точке C :  Остается приравнять |CD| к L - длине биссектрисы:
Остается приравнять |CD| к L - длине биссектрисы:


Думаю, что объяснять, как производятся дальнейшие построения, не нужно
Думаю, что объяснять, как производятся дальнейшие построения, не нужно
Приложения:
8Rd вы как строите ( чтобы проще?) , какие отрезки берете? :)
Решение с углами не рассматривал, не хотелось с ними напрягаться. Тоже хорошее решение. И у меня еще одно есть.... В общем, всем спасибо.....
Я сначала строю корень из 2R*2d, скажем, как высоту прямоугольного треугольника по известным отрезкам гипотенузы, затем умножаю результат на корень из 2 с помощью равнобедренного прямоугольного треугольника, затем ищу гипотенузу по катетам
А давайте помещу задачу для Вас?
так давайте, все порешают..
Я послал Вам ссылку
видел, думал другая какая-то задача. Сейчас выложу решение
Похожие вопросы
1 год назад
1 год назад
2 года назад