В правильной четырёхугольной пирамиде боковое ребро образует с плоскостью основания угол 45 градусов. Сторона основания пирамиды равна 6 см. Найдите объем пирамиды

Можно с рисунком

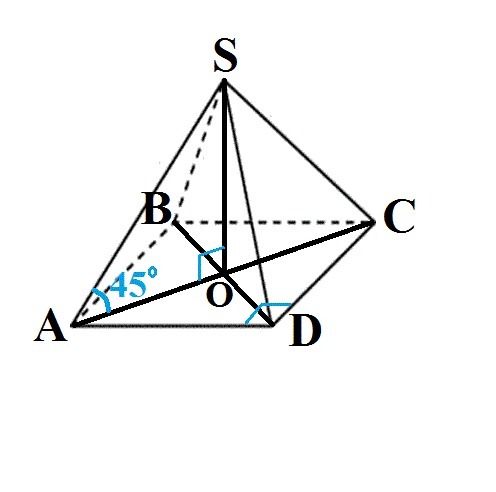
В основании правильной четырехугольной пирамиды SABCD лежит правильный четрехугольник (квадрат) со стороной AB=BC=CD=AD= 6cм. 
Высота (SO) опущена в точку пересечения диагоналей основания. 

В прямоугольном треугольнике AOS:
∠SO = 90°
∠SAO = 45°
∠ASO = 180 - 90 - 45 = 45 (°) 
⇒ треугольник AOS - прямоугольный равнобедренный с основанием-гипотенузой AS, равными боковыми сторонами-катетами AO=SO
⇒ высота (SO) равна половине длины диагонали основания (т.к. диагонали квадрата точкой пересечения делятся пополам)

Длина диагонали (d) квадрата со стороной (а)
d = a√2
SO = d / 2
SO = AB * √2 / 2
SO = 6 * √2 / 2 = 3√2 (cм)

Объем пирамиды
V = 1/3 * S * h, где S - площадь основания пирамиды, h - высота пирамиды

S = AB²
S = 6² = 36 (cм²)

V = 1/3 * 36 * 3√2 = 36√2 (см³)