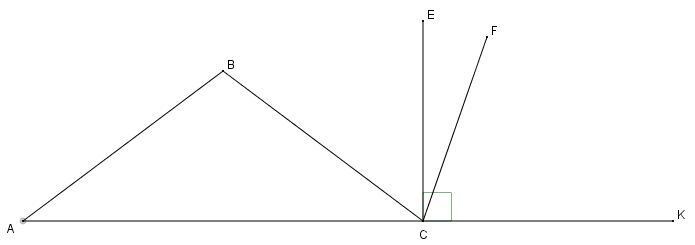
В равнобедренном треугольнике АВС с основанием АС угол при вершине равен 40°. Из вершины внешнего угла ВСК проведены биссектриса CF и луч СЕ, перпендикулярный АК. Найдите градусную меру угла FCE.

Ответ: 35°

Объяснение:

У равнобедренного треугольника углы при основании равны, т.е.

∠BAC = ∠BCA = (180° - ∠ABC)/2 = (180° - 40°)/2 = 70°

∠BCA и ∠BCK - смежные ⇒ ∠BCK = 180° - 70° = 110°.

Поскольку CF — биссектриса угла BCK, то ∠BCF = ∠FCK = 55°.

∠ECK = ∠FCE + ∠FCK ⇒ ∠FCE = 90° - 55° = 35°.