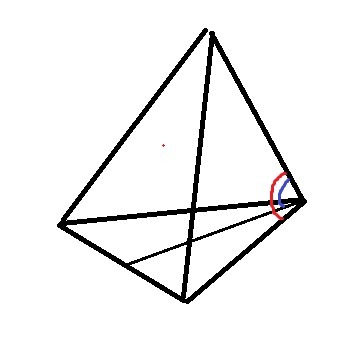
Равны ли эти углы? Если да, по какому свойству/теореме?
Синий угол - это угол наклона бокового ребра к плоскости
Пирамида правильная

Красный угол равен 60, т.к. треугольник равносторонний.
Найдём, чему равен синий угол. Для этого опустим из вершины пирамиды высоту. Высота пирамиды проектируется в точку пересечения медиан (высот, биссектрис) основания (которое у нас равносторонний треугольник). А точка пересечения высот (медиан, биссектрис) правильного треугольника делит каждую из них в отношении 2:1, считая от вершины.
Высота треугольного основания равна √3 *a /2, где a - сторона треугольника (или ребро пирамиды). Значит, расстояние от вершины, до точки пересечения высот равна (√3 *a/2) : (3/2) = √3 *a/3.
Теперь можно вычислить косинус синего угла по катету и гипотенузе приямоугольного треугольника, образованного высотой пирамиды, ребром (а) и частью высоты треугольного основания (√3*а/3)
cos(α) = (√3*a/3)/a = √3/3 = 0.577
cos(60) = 0.5
Чем больше косинус угла, тем меньше угол. Следовательно, синий угол меньше красного (примерно равен 54,7 градусов).

Для правильной пирамиды это правильное решение. Но фокус в том, что синий угол меньше красного при любом виде пирамиды и при любом угле наклона бокового ребра к плоскости основания. Чтобы это понять, нужно поворачивать сторону основания в плоскости. Когда отрезок находится в положении проекции бокового ребра на плоскость, угол - синий - минимальный.

Синий угол меньше красного не при любом виде пирамиды. В некоторых случаях эти углы равны. Например, если в основании прямоугольный треугольник.

Честно сказать, не понимаю, как форма треугольника в основании может влиять на угол наклона бокового ребра к плоскости. А вот если боковое ребро перпендикулярно к плоскости основания, тогда да, угол всегда равен 90

Если в основания прямоугольный треугольник, то высота совпадёт со стороной основания и синий с красным углом будут равны.