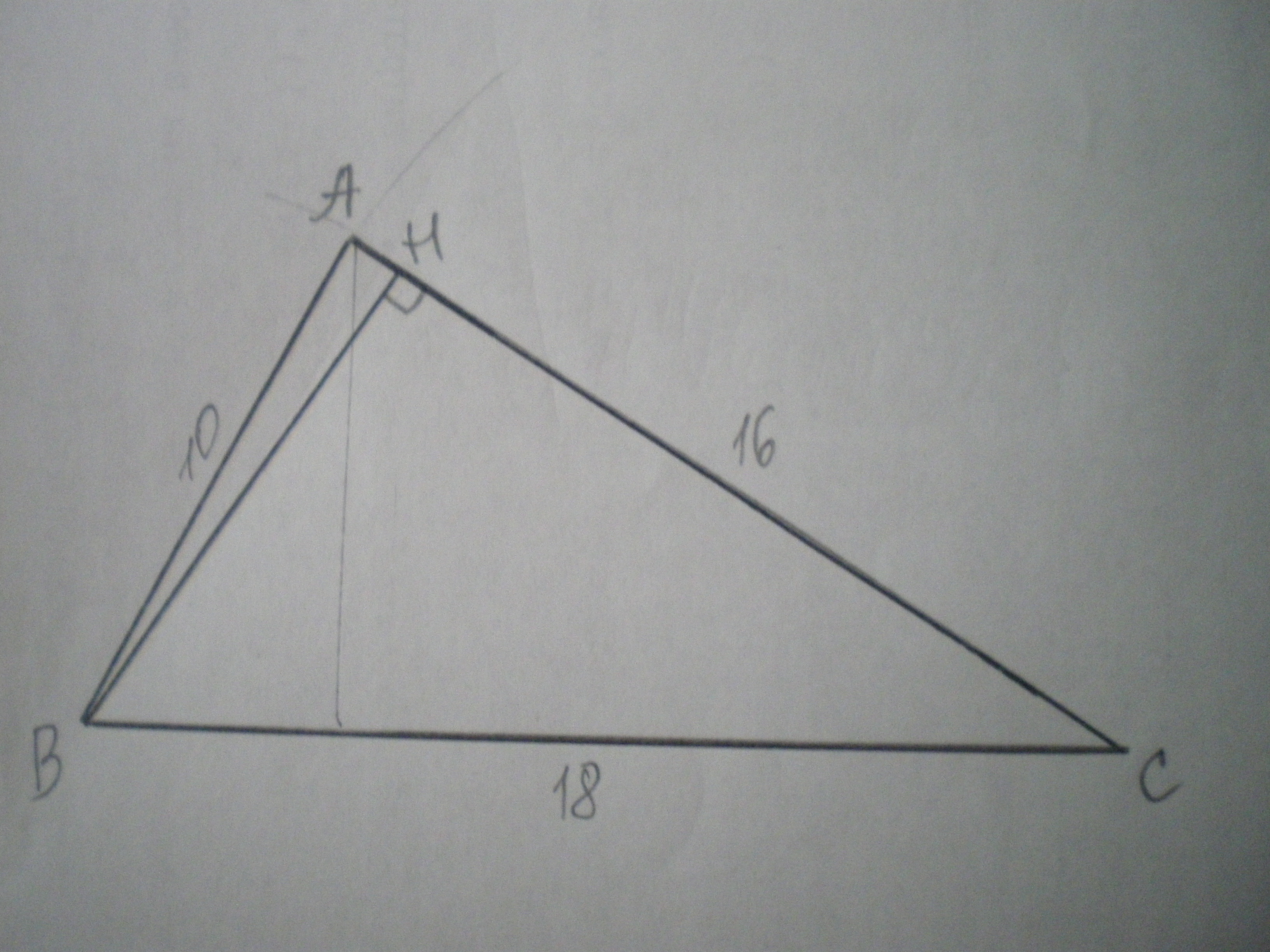
з точки до прямої проведено дві похилі завдовжки 10 см і 18 см, а сума їх проекцій на пряму дорівнює 16 см. Знайти відстань від даної точки до цієї прямої

Дано: пряма АС, АВ і ВС - похилі, АВ=10 см, ВС=18 см. Знайти ВН.

Маємо ΔАВС, де АВ=10 см, ВС=18 см, АС=16 см. ВН - висота.

АН - проекція АВ на АС, СН - проекція ВС на АС. Нехай АН=х см, тоді СН=16-х см.

Знайдемо ВН за теоремою Піфагора. ВН²=АВ²-АН²=100-х², або

ВН²=ВС²-(16-х)²=324-(256-32х+х²); тоді 100-х²=324-(256-32х+х²);

100-х²=324-256+32х-х²; 32х=32; х=1.

АН=1 см, СН=16-1=15 см.

Знайдем ВН из ΔАВН; ВН=√(100-1)=√99≈9,95 см.

Є простіше рішення за формулою Герона

S(ABC)=√(p(p-a)(p-b)(p-c)=√(22*12*4*6)=√6336≈79,6.

S(ABC)=12 * AC * BH; 12 * 16 * ВН=79,6; 8ВН=79,6; ВН=9,95 см.