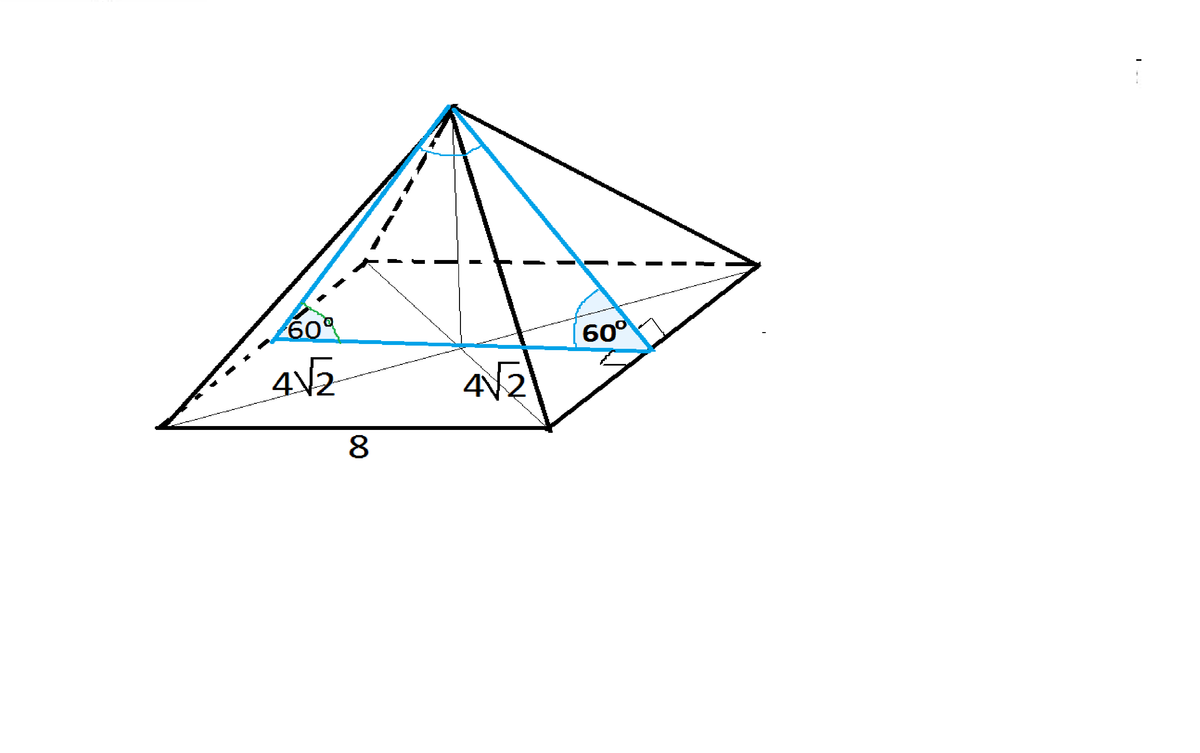
В правильной четырехугольной пирамиде диагональ основания равно 8 корней из 2 см, а двугранный угол при основании 60 градусов. Найдите площадь полной поверхности пирамиды
Ответы
Ответ дал:
0
При длине стороны а диагональ квадрата всегда а√2.
Поэтому, если диагональ основания - квадрата - равна 8√2 см, сторона основания равна 8 см.
Так как двугранный угол при основании равен 60°, сечение пирамиды, содержащее высоту - правильный треугольник.
Отсюда апофема каждой грани равна длине стороны основания.
Апофема=8 см.
Площадь полной поверхности - сумма площади основания и площади всех четырех граней.
S осн=a²
S бок=4*а*h:2
S бок=4*8*8:2=128 см²
S осн=8*8=64 см
S полн=128+64=192 см²
Поэтому, если диагональ основания - квадрата - равна 8√2 см, сторона основания равна 8 см.
Так как двугранный угол при основании равен 60°, сечение пирамиды, содержащее высоту - правильный треугольник.
Отсюда апофема каждой грани равна длине стороны основания.
Апофема=8 см.
Площадь полной поверхности - сумма площади основания и площади всех четырех граней.
S осн=a²
S бок=4*а*h:2
S бок=4*8*8:2=128 см²
S осн=8*8=64 см
S полн=128+64=192 см²
Приложения:
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад