Хорда окружности равна 10. Через один конец хорды проведена касательная к окружности, а через другой — секущая, параллельная касательной. Найдите радиус окружности, если внутренний отрезок секущей равен 12.

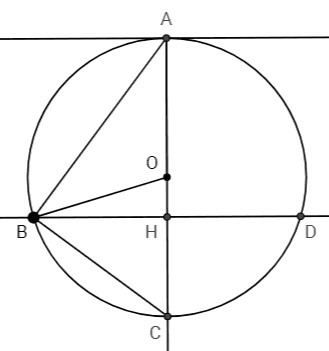
Диаметр AC делит хорду BD пополам (диаметр AC перпендикулярен касательной, BD параллелен касательной => AC⊥BD, BO=OD (радиусы) => AC - серединный перпендикуляр к BD)
BH= BD/2 = 12/2 =6

AB^2=BH^2 +AH^2 <=> AH= √(100-36) =8

Угол ABC прямой, т.к. опирается на диаметр. BH - высота в △ABC. Высота из вершины прямого угла равна произведению проекций катетов.
BH^2 = AH*CH <=> 36= AH*CH <=> CH= BH^2/AH = 36/8 =4,5

AC= AH+CH = 8+4,5 =12,5
R= AC/2 =12,5/2 =6,25