найдите объём правильной треугольной пирамиды равна 8 см , а в двугранный угол при основании равен 60°. найдите объём пирамиды .

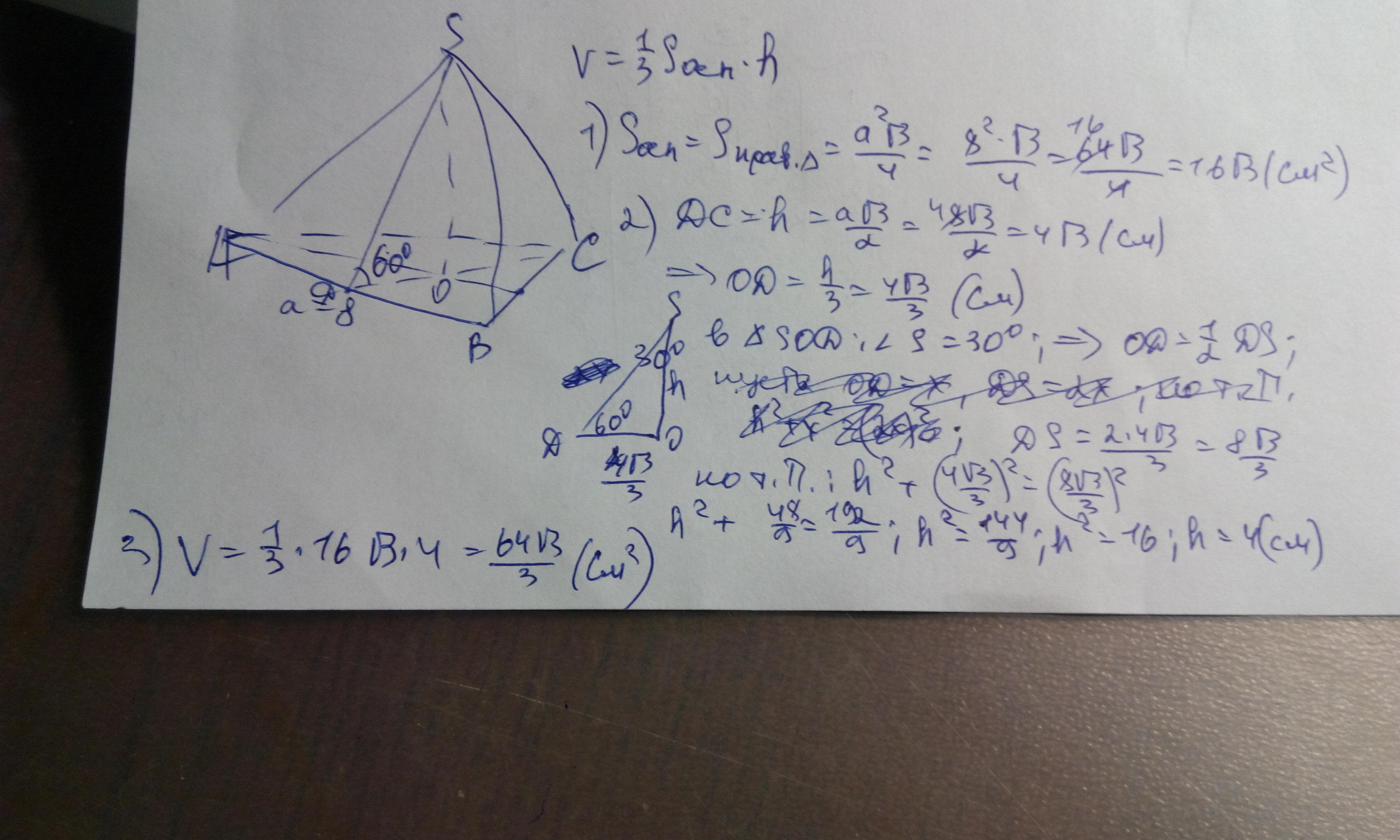
Решение дано на фото.

Пусть дано:
 - сторона а основания правильной треугольной пирамиды равна 8 см,
 - двугранный угол α при основании равен 60°.

Находим высоту h основания:
h = a*cos 30° = 8*(√3/2) = 4√3 см.
Основанием высоты пирамиды эта высота делится в отношении 2:1 от вершины треугольника в основании пирамиды.
(1/3)h = 4√3/3 см.
Находим высоту пирамиды:
Н =(1/3)h*tg α = (4√3/3)*√3 = 4 см.
Площадь So основания равна:
So = a²√3/4 =64√3/4 = 16√3 см².
Объём пирамиды равен:
V = (1/3)So*H = (1/3)*16√3*4 = 64√3/3 ≈  36,95042 см³.