ПОЖАЛУЙСТА... РЕШИТЕ УРАВНЕНИЕ... 25 баллов...

Приложения:

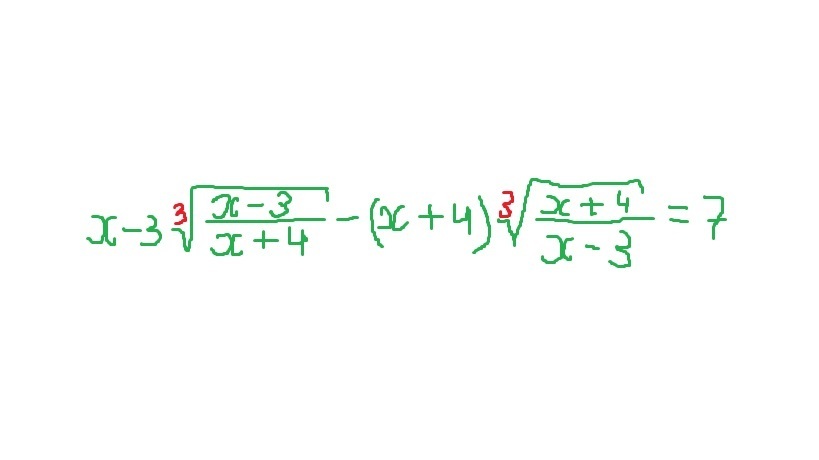
terepanatalia: скобки не потеряли в х-3

specnaz12: дааа скобки там

Mr0leg: В следующий раз постарайтесь дать условие без ошибок!

Ответы

Ответ дал: Аноним

$\displaystyle (x-3) \sqrt[3]{ \frac{x-3}{x+4} } -(x+4) \sqrt[3]{ \frac{x+4}{x-3} }=7$

Представим правую часть уравнения так:

$\displaystyle (x-3)\sqrt[3]{ \frac{x-3}{x+4} }-(x+4)\sqrt[3]{ \frac{x+4}{x-3} }=x+4-(x-3)\,\,\, |:(x-3\ne0)\\ \\ \\ \sqrt[3]{ \frac{x-3}{x+4} }- \frac{x+4}{x-3} \sqrt[3]{ \frac{x+4}{x-3} }= \frac{x+4}{x-3} -1$

Пусть $\sqrt[3]{ \dfrac{x+4}{x-3} }=t;\,\,\,\,\, \Rightarrow\,\,\,\,\, \dfrac{x+4}{x-3}=t^3$

Тогда имеем

$\frac{1}{t} -t^3\cdot t=t^3-1 |\cdot t\\ \\ 1-t^5=t^4-t\\ \\ t^5+t^4-t-1=0\\ t^4(t+1)-(t+1)=0\\ \\ (t+1)(t^4-1)=0\\ (t+1)(t^2-1)(t^2+1)=0\\ (t+1)^2(t-1)(t^2+1)=0\\ t_1=-1\\ t_2=1$

Обратная замена

$\sqrt[3]{ \dfrac{x+4}{x-3} }=-1\\ \\ x+4=-x+3\\ 2x=-1\\ x=-0.5\\ \\ \\ \sqrt[3]{ \dfrac{x+4}{x-3} }=1\\ \\ x+4=x-3\\ 4=-3$

Ответ: -0.5

specnaz12: СПАСИБООООО!!!

Похожие вопросы

Другие предметы

1 год назад

Що називають емпатією, чому для людини важливо вміти її проявляти

Математика

1 год назад

РЕШИТЕ СРОЧНО! ТУТ ИЗИ! 70 БАЛОВ ДАЮ!

Алгебра

1 год назад

Обчислити в зручний способ 95×85

Русский язык