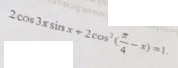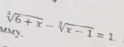Ответы
Ответ дал:
0
2сos3xsinx+2cos(π/2-x)=1
2*1/2*(sin(x-3x)+sin(x+3x))+2*(1+cos(π/2-2x)/2=1
sin(-2x)+sin4x+1+sin2x=1
-sin2x+sin4x+sin2x=1-1
sin4x=0
4x=πk
x=πk/4,k∈z
√(6+x)-√(x-1)=1
ОДЗ
{6+x≥0⇒x≥-6
{x-1≥0⇒x≥1
x∈[1;∞)
√(6+x)=1+√(x-1)
возведем в квадрат
6+x=1+2√(x-1)+x-1
2√(x-1)=6
√(x-1)=3
x-1=9
x=9+1
x=10
2*1/2*(sin(x-3x)+sin(x+3x))+2*(1+cos(π/2-2x)/2=1
sin(-2x)+sin4x+1+sin2x=1
-sin2x+sin4x+sin2x=1-1
sin4x=0
4x=πk
x=πk/4,k∈z
√(6+x)-√(x-1)=1
ОДЗ
{6+x≥0⇒x≥-6
{x-1≥0⇒x≥1
x∈[1;∞)
√(6+x)=1+√(x-1)
возведем в квадрат
6+x=1+2√(x-1)+x-1
2√(x-1)=6
√(x-1)=3
x-1=9
x=9+1
x=10
skvrttt:
во втором корни третьей степени, если чё
халтурщина!
Ответ дал:
0
первое уравнение, ответ: 
; решение:
![2cos3xsinx+2cos^2(\frac{\pi}{4}-x)=1;~2cos3xsinx+2*\frac{1+cos[2(\frac{\pi}{4}-x)]}{2}=1;~\\2(4cos^3x-3cosx)sinx+cos(\frac{\pi}{2}-2x)=0;~2[cosx(4cos^2x-3)]sinx+\\sin2x=0;~2sinxcosx[4(1-sin^2x)-3]+sin2x=0;~\\sin2x[1-4sin^2x]+sin2x=0;~sin2x(1-4sin^2x+1)=0;~\\sin2x[2(1-2sin^2x)]=0;~sin2xcos2x=0;~sin4x=0\\\\4x=n\pi,n\in Z~\to~x=\frac{n\pi}{4},n\in Z](https://tex.z-dn.net/?f=2cos3xsinx%2B2cos%5E2%28%5Cfrac%7B%5Cpi%7D%7B4%7D-x%29%3D1%3B%7E2cos3xsinx%2B2%2A%5Cfrac%7B1%2Bcos%5B2%28%5Cfrac%7B%5Cpi%7D%7B4%7D-x%29%5D%7D%7B2%7D%3D1%3B%7E%5C%5C2%284cos%5E3x-3cosx%29sinx%2Bcos%28%5Cfrac%7B%5Cpi%7D%7B2%7D-2x%29%3D0%3B%7E2%5Bcosx%284cos%5E2x-3%29%5Dsinx%2B%5C%5Csin2x%3D0%3B%7E2sinxcosx%5B4%281-sin%5E2x%29-3%5D%2Bsin2x%3D0%3B%7E%5C%5Csin2x%5B1-4sin%5E2x%5D%2Bsin2x%3D0%3B%7Esin2x%281-4sin%5E2x%2B1%29%3D0%3B%7E%5C%5Csin2x%5B2%281-2sin%5E2x%29%5D%3D0%3B%7Esin2xcos2x%3D0%3B%7Esin4x%3D0%5C%5C%5C%5C4x%3Dn%5Cpi%2Cn%5Cin+Z%7E%5Cto%7Ex%3D%5Cfrac%7Bn%5Cpi%7D%7B4%7D%2Cn%5Cin+Z "2cos3xsinx+2cos^2(\frac{\pi}{4}-x)=1;~2cos3xsinx+2*\frac{1+cos[2(\frac{\pi}{4}-x)]}{2}=1;~\\2(4cos^3x-3cosx)sinx+cos(\frac{\pi}{2}-2x)=0;~2[cosx(4cos^2x-3)]sinx+\\sin2x=0;~2sinxcosx[4(1-sin^2x)-3]+sin2x=0;~\\sin2x[1-4sin^2x]+sin2x=0;~sin2x(1-4sin^2x+1)=0;~\\sin2x[2(1-2sin^2x)]=0;~sin2xcos2x=0;~sin4x=0\\\\4x=n\pi,n\in Z~\to~x=\frac{n\pi}{4},n\in Z")
второе уравнение, ответ:
; решение:
![\sqrt[3]{x+6}-\sqrt[3]{x-1}=1;~(\sqrt[3]{x+6})^3=(\sqrt[3]{x-1}+1)^3;~\\x+6=(\sqrt[3]{x-1})^3+3(\sqrt[3]{x-1})^2+3(\sqrt[3]{x-1})+1;~\\x+6=x-1+3(\sqrt[3]{x-1})^2+3(\sqrt[3]{x-1})+1;~\\(\sqrt[3]{x-1})^2+(\sqrt[3]{x-1})-2=0;~[\sqrt[3]{x-1}=a]~a^2+a-2=0~\to\\\left[\begin{array}{ccc}a_1=-2\\a_2=1\end{array}\right\to\left[\begin{array}{ccc}\sqrt[3]{x-1}=-2\\\sqrt[3]{x-1}=1\end{array}\right\to\left[\begin{array}{ccc}x-1=-8\\x-1=1\end{array}\right\to\left[\begin{array}{ccc}x_1=-7\\x_2=2\end{array}\right](https://tex.z-dn.net/?f=%5Csqrt%5B3%5D%7Bx%2B6%7D-%5Csqrt%5B3%5D%7Bx-1%7D%3D1%3B%7E%28%5Csqrt%5B3%5D%7Bx%2B6%7D%29%5E3%3D%28%5Csqrt%5B3%5D%7Bx-1%7D%2B1%29%5E3%3B%7E%5C%5Cx%2B6%3D%28%5Csqrt%5B3%5D%7Bx-1%7D%29%5E3%2B3%28%5Csqrt%5B3%5D%7Bx-1%7D%29%5E2%2B3%28%5Csqrt%5B3%5D%7Bx-1%7D%29%2B1%3B%7E%5C%5Cx%2B6%3Dx-1%2B3%28%5Csqrt%5B3%5D%7Bx-1%7D%29%5E2%2B3%28%5Csqrt%5B3%5D%7Bx-1%7D%29%2B1%3B%7E%5C%5C%28%5Csqrt%5B3%5D%7Bx-1%7D%29%5E2%2B%28%5Csqrt%5B3%5D%7Bx-1%7D%29-2%3D0%3B%7E%5B%5Csqrt%5B3%5D%7Bx-1%7D%3Da%5D%7Ea%5E2%2Ba-2%3D0%7E%5Cto%5C%5C%5Cleft%5B%5Cbegin%7Barray%7D%7Bccc%7Da_1%3D-2%5C%5Ca_2%3D1%5Cend%7Barray%7D%5Cright%5Cto%5Cleft%5B%5Cbegin%7Barray%7D%7Bccc%7D%5Csqrt%5B3%5D%7Bx-1%7D%3D-2%5C%5C%5Csqrt%5B3%5D%7Bx-1%7D%3D1%5Cend%7Barray%7D%5Cright%5Cto%5Cleft%5B%5Cbegin%7Barray%7D%7Bccc%7Dx-1%3D-8%5C%5Cx-1%3D1%5Cend%7Barray%7D%5Cright%5Cto%5Cleft%5B%5Cbegin%7Barray%7D%7Bccc%7Dx_1%3D-7%5C%5Cx_2%3D2%5Cend%7Barray%7D%5Cright "\sqrt[3]{x+6}-\sqrt[3]{x-1}=1;~(\sqrt[3]{x+6})^3=(\sqrt[3]{x-1}+1)^3;~\\x+6=(\sqrt[3]{x-1})^3+3(\sqrt[3]{x-1})^2+3(\sqrt[3]{x-1})+1;~\\x+6=x-1+3(\sqrt[3]{x-1})^2+3(\sqrt[3]{x-1})+1;~\\(\sqrt[3]{x-1})^2+(\sqrt[3]{x-1})-2=0;~[\sqrt[3]{x-1}=a]~a^2+a-2=0~\to\\\left[\begin{array}{ccc}a_1=-2\\a_2=1\end{array}\right\to\left[\begin{array}{ccc}\sqrt[3]{x-1}=-2\\\sqrt[3]{x-1}=1\end{array}\right\to\left[\begin{array}{ccc}x-1=-8\\x-1=1\end{array}\right\to\left[\begin{array}{ccc}x_1=-7\\x_2=2\end{array}\right")
второе уравнение, ответ:
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад