в треугольнике ABC стороны AB,BC и AC равны соответственно 4 ,5 и 6На стороне AC находится центр окружности, касающейся сторон AB и BC.найдите произведение длин отрезков, на которые центр окружности делит сторону AC

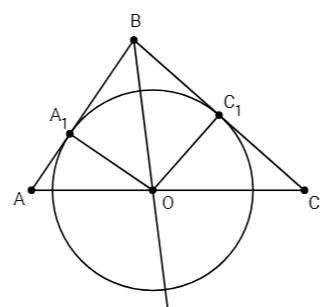
Отрезки касательных к окружности (BA1, BC1), проведенных из одной точки, равны и составляют равные углы с прямой (BO), проходящей через эту точку и центр окружности.
∠A1BO=∠C1BO, BO - биссектриса ∠ABC.

Биссектриса при вершине треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам.
AO/OC = AB/BC = 4/5

AO*OC= 4/9 *AC *5/9 *AC = 20*36/81 = 80/9 = 8 8/9 (~8,89)