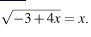Предмет: Алгебра
Автор: mrfullmetal15
Вопрос задан 1 год назад

Помогите решить уравнение)

Приложения:

Ответы

Ответ дал: Асик777Асик

$\sqrt{-3+4x}=x\\-3+4x=x^{2}\\x^{2}-4x+3=0\\x_{1}*x_{2}=3\\x_{1}+x_{2}=4\\$
Получается: х₁=1, х₂=3. Ответ: корни уравнения- это 1 и 3.

Disaczar: уравнение иррациональное _ нужно искать ОДЗ

Асик777Асик: Я знаю, но если бы какой-то корень не удовлетворял, я бы заметил, просто я раньше нашел корни.

Ответ дал: Disaczar

для этого уравнения для начала найдём ОДЗ, ибо оно иррациональное
$x \geq \frac{3}{4}$
теперь можно решать само уравнение
$\sqrt{-3 + 4x} = x \\ -3 + 4x = x^{2} \\ x^{2} - 4x + 3 = 0$
решим по теореме Виета
$\left \{ {{x_{1} + x_{2} = 4} \atop {x_{1} + x_{2} = 3}} \right.$
и получаем корни
$x_{1} = 3; x_{2} = 1$
сверяем корни с ОДЗ. они удовлетворяют ОДЗ, поэтому x = 1 и 3

Disaczar: невнимательно написал т. Виета. там во втором случае стоит знак '*'

Disaczar: ой.

Disaczar: там оба корня проходят через ОДЗ

Disaczar: 3 и 1 корни.

Похожие вопросы

Қазақ тiлi

1 год назад

1992 жылы 12 қарашада еліміздің Президенті Нұрсұлтан Әбішұлы Назарба- ев «Қазақстан Республикасында валю- та енгізу туралы Жарлыққа» қол қойды. Ескі ақшаны ұлттық теңгеге айырбастау 15 қарашадан

Литература

1 год назад

Лучшие моменты из повести Гобсек Бальзака(3 лучших момента)

Информатика