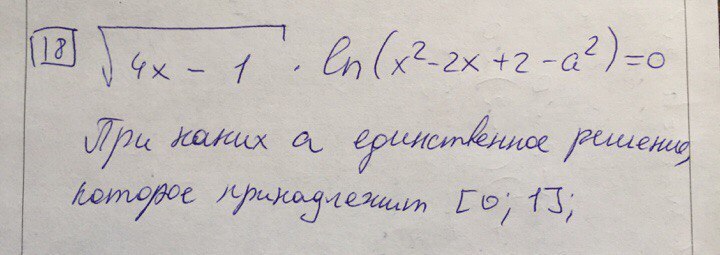Ответы
Ответ дал:
0
Произведение равно нулю, если один из множителей равен нулю, т.е.  откуда
откуда  и
и 

Пользуясь формулой сокращенного умножения , получим
, получим  откуда
откуда 
Вычислим ОДЗ уравнения.
1) Подкоренное выражение принимает неотрицательные значения, т.е. откуда
откуда  .
.
2) Под логарифмическое выражение больше нуля, т.е.
Видим, что корень![x= frac{1}{4} in [0;1] x= frac{1}{4} in [0;1]](https://tex.z-dn.net/?f=x%3D+frac%7B1%7D%7B4%7D+in+%5B0%3B1%5D) и принадлежит ОДЗ. Также две другие корни пусть не удовлетворяют ОДЗ при
и принадлежит ОДЗ. Также две другие корни пусть не удовлетворяют ОДЗ при  , т.е.
, т.е. 
Подставив х=1/4 в ОДЗ под логарифмического выражения, получаем откуда
откуда 
Общее решение есть промежуток
есть промежуток 
Проверим при а=±3/4. Если а=±3/4, то корни уравнения будут![x_1=0.25in[0;1] x_1=0.25in[0;1]](https://tex.z-dn.net/?f=x_1%3D0.25in%5B0%3B1%5D) и
и ![x_2=1.75notin[0;1]. x_2=1.75notin[0;1].](https://tex.z-dn.net/?f=x_2%3D1.75notin%5B0%3B1%5D.)
Уравнение имеет единственное решение на отрезке [0;1] при![a in bigg(-dfrac{5}{4} ;-dfrac{3}{4} bigg]cupbigg[dfrac{3}{4} ;dfrac{5}{4} bigg). a in bigg(-dfrac{5}{4} ;-dfrac{3}{4} bigg]cupbigg[dfrac{3}{4} ;dfrac{5}{4} bigg).](https://tex.z-dn.net/?f=a+in+bigg%28-dfrac%7B5%7D%7B4%7D+%3B-dfrac%7B3%7D%7B4%7D+bigg%5Dcupbigg%5Bdfrac%7B3%7D%7B4%7D+%3Bdfrac%7B5%7D%7B4%7D+bigg%29.)
Пользуясь формулой сокращенного умножения
Вычислим ОДЗ уравнения.
1) Подкоренное выражение принимает неотрицательные значения, т.е.
2) Под логарифмическое выражение больше нуля, т.е.
Видим, что корень
Подставив х=1/4 в ОДЗ под логарифмического выражения, получаем
Общее решение
Проверим при а=±3/4. Если а=±3/4, то корни уравнения будут
Уравнение имеет единственное решение на отрезке [0;1] при
Похожие вопросы
2 года назад
2 года назад
6 лет назад
6 лет назад
9 лет назад
9 лет назад
9 лет назад