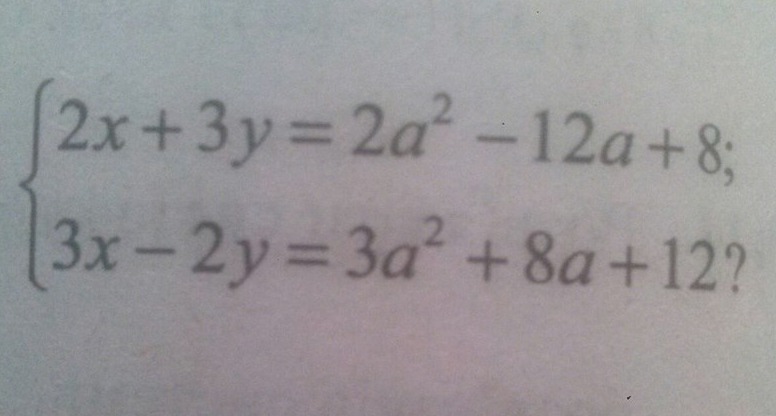Ответы
Ответ дал:
8
До першого рівняння домножимо на 2, а друге на 3, маємо

Додавши обидві рівняння, маємо:

Тоді

 . Звідки при а = 2, сума х+у набуває найменшого значення
. Звідки при а = 2, сума х+у набуває найменшого значення
Відповідь: а=2.
Додавши обидві рівняння, маємо:
Тоді
Відповідь: а=2.
Ответ дал:
0
Рассмотрите такой вариант (по возможности перепроверьте арифметику):
1) в системе уравнений выразить через а х и у:

Пояснение: сначала первое уравнение умножить на 3, а второе - на (-2) и сложить оба уравнения (получится 13у=...), затем первое уравнение умножить на 2, а второе - на 3, и оба уравнения сложить (получится 13х=...).
2) из полученной системы можно выразить сумму х+у:
x+y=a²-4a+4, откуда можно найти наименьшую сумму, зная формулу для нахождения ординаты вершины параболы (ордината_вершины= -D/4a):

То есть при а=2 сумма х+у=0 - наименьшая (х=8, у=-8).
1) в системе уравнений выразить через а х и у:
Пояснение: сначала первое уравнение умножить на 3, а второе - на (-2) и сложить оба уравнения (получится 13у=...), затем первое уравнение умножить на 2, а второе - на 3, и оба уравнения сложить (получится 13х=...).
2) из полученной системы можно выразить сумму х+у:
x+y=a²-4a+4, откуда можно найти наименьшую сумму, зная формулу для нахождения ординаты вершины параболы (ордината_вершины= -D/4a):
То есть при а=2 сумма х+у=0 - наименьшая (х=8, у=-8).
Просьба модератору вернуть на доработку: ошибка во втором уравнении системы.
Или удалите решение, так как верное уже есть. Спасибо.
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад