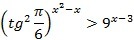Предмет: Алгебра
Автор: markys8695
Вопрос задан 8 лет назад

Найдите число целых решений неравенства

Приложения:

Ответы

Ответ дал: Асик777Асик

$tg^2 frac{ pi }{6}=tg^230=( frac{1}{ sqrt{3}})^2= frac13$
$( frac13)^{x^2}^-^x textgreater 9^x^-^3\ (9)^- ^frac12= frac13\ (9)^- ^frac12^*^(^{x^2}^-^x^) textgreater 9^x^-^3\ - frac12(x^2-x) textgreater x-3\ x^2-x textless (x-3):(- frac12)\ x^2-x textless -2(x-3)\ x^2-x textless -2x+6\ x^2-x+2x-6 textless 0\ x^2+x-6 textless 0\ x^2+x-6=0\ x_1*x_2=-6\ x_1+x_2=-1\ x_1=-3\ x_2=2\ $
Сейчас отметим всё на интервале:
+ _ +
______-3_________2_________ Обе точки пустые.
Выбираем отрицательный интервал, и получится:
Ответ: (-3;2). Тогда количество целых решений равно: 4→конечный ответ).

Похожие вопросы

Русский язык

2 года назад

Ребята, напишите маленький рассказ по теме "Поделитесь своими впечатлениями в зоопарке или в цирке". Заранее спасибо большое!

Окружающий мир

2 года назад

Какое значение имеют растения для всех обитателей нашей планеты

Русский язык

6 лет назад

в каком предложении перед союзом и нужна запятая? 1) дети прыгали по ступеням и громко смеялись. 2) закончились каникулы и школа вновь открыла свои двери. 3) мама забыла зонт в машине и таксист

Русский язык

6 лет назад