Площадь треугольника ABC равна 40 см^2. На медиане AM обозначили точку P так, что AP : PM = 2 : 3 . Найдите S треугольника BPM.
Знаю, что тут задача решается через свойства площади треугольника, но подзабыл как именно.

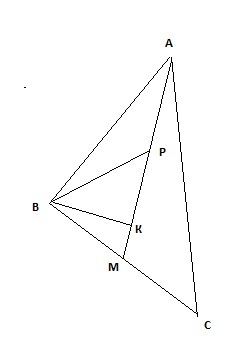
Построим треугольник АВС, площадь которого равна 40 кв. см, Проведем медиану АМ. и обозначим точу Р такую, что АР:РМ=2:3.

Так как медиана треугольника делит его на две равновеликие части, то Sавм=40/2=20 кв. см.

Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).  

Для наглядности построим высоту ВК – она будет являться высотой как для треугольника ВАМ так и для треугольника ВРМ

Основания Данных треугольников будут соотноситься как 3:5, значит

Sврм : Sвам=3 : 5

Sврм= Sвам*3 / 5=20*3/5=12 кв.см.