Ответы
Ответ дал:
5
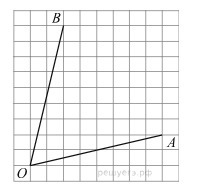
Найдём OB по теореме Пифагора:

Далее найдём AO по теореме Пифагора:

Найдем BA так же:

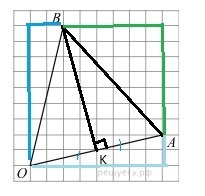
Так как треуг. OAB-равнобедренный=>Высота, проведенная из вершины B-медиана и бис-са
OK=
BK=
Отсюда можем найти тангенс угла AOB:


Далее найдём AO по теореме Пифагора:
Найдем BA так же:
Так как треуг. OAB-равнобедренный=>Высота, проведенная из вершины B-медиана и бис-са
OK=
BK=
Отсюда можем найти тангенс угла AOB:
Приложения:
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад