Предмет: Математика
Автор: BonyaLA
Вопрос задан 8 лет назад

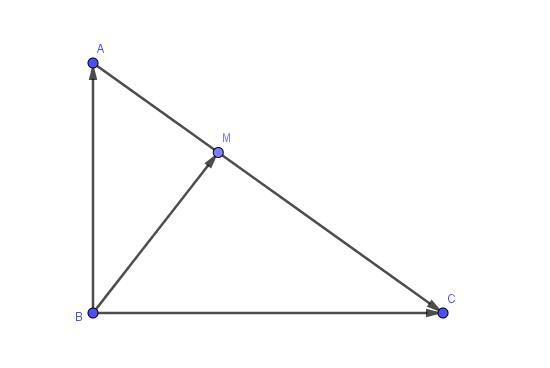
Точка М делит гипотенузу АС прямоугольного треугольника АВС в отношении АМ:МС=2:3. Найдите разложение вектора ВМ по векторам ВА и ВС и длину вектора ВМ, если АВ=10 см, СВ=5 см.

Ответы

Ответ дал: Аноним

Из условия $dfrac{AM}{MC}=dfrac{2}{3}$ , тогда $overrightarrow{AM}=dfrac{2}{5}overrightarrow{AC}$

По правилу треугольника $overrightarrow{AC}=-overrightarrow{BA}+overrightarrow{BC}$

Далее снова по правилу треугольника ABM:

$overrightarrow{BM}=-overrightarrow{BA}+overrightarrow{AM}=-overrightarrow{BA}+dfrac{2}{5}overrightarrow{AC}=-overrightarrow{BA}+dfrac{2}{5}overrightarrow{BC}-dfrac{2}{5}overrightarrow{BA}=dfrac{2}{5}overrightarrow{BC}-dfrac{7}{5}overrightarrow{BA}$

Поскольку векторы BA и BC перпендикулярны, то их скалярное произведение равно нулю, следовательно,

$left|overrightarrow{BM}right|=sqrt{left(dfrac{2}{5}overrightarrow{BC}-dfrac{7}{5}overrightarrow{BA}right)^2}=sqrt{dfrac{4}{25}BC^2+dfrac{49}{25}BA^2}=sqrt{4+196}=10sqrt{2}~_{sf CM}$