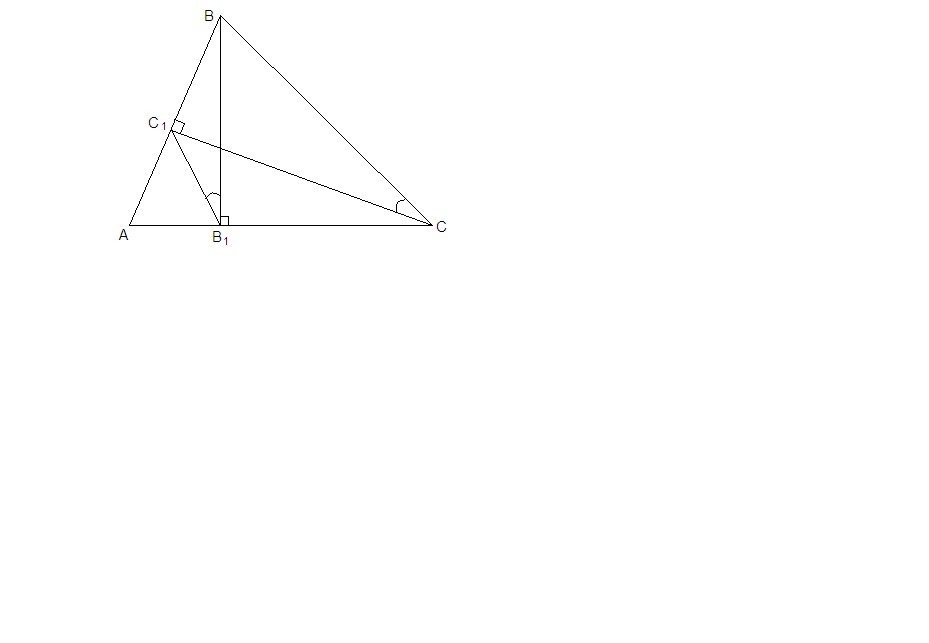
В остроугольном треугольнике АВС проведены высоты ВВ1 и СС1. Докажите, что углы ВВ1С1 и ВСС1 равны. Спасибо.

Центр окружности, описанной около прямоугольного треугольника, лежит на середине его гипотенузы.
Треугольники ВВ₁С и ВС₁С - прямоугольные с общей гипотенузой ВС. Поэтому если построить окружность с диаметром ВС, точки В₁ и С₁ будут лежать на этой окружности.
Тогда ∠ВВ₁С₁ = ∠ВСС₁ как вписанные, опирающиеся на одну дугу.