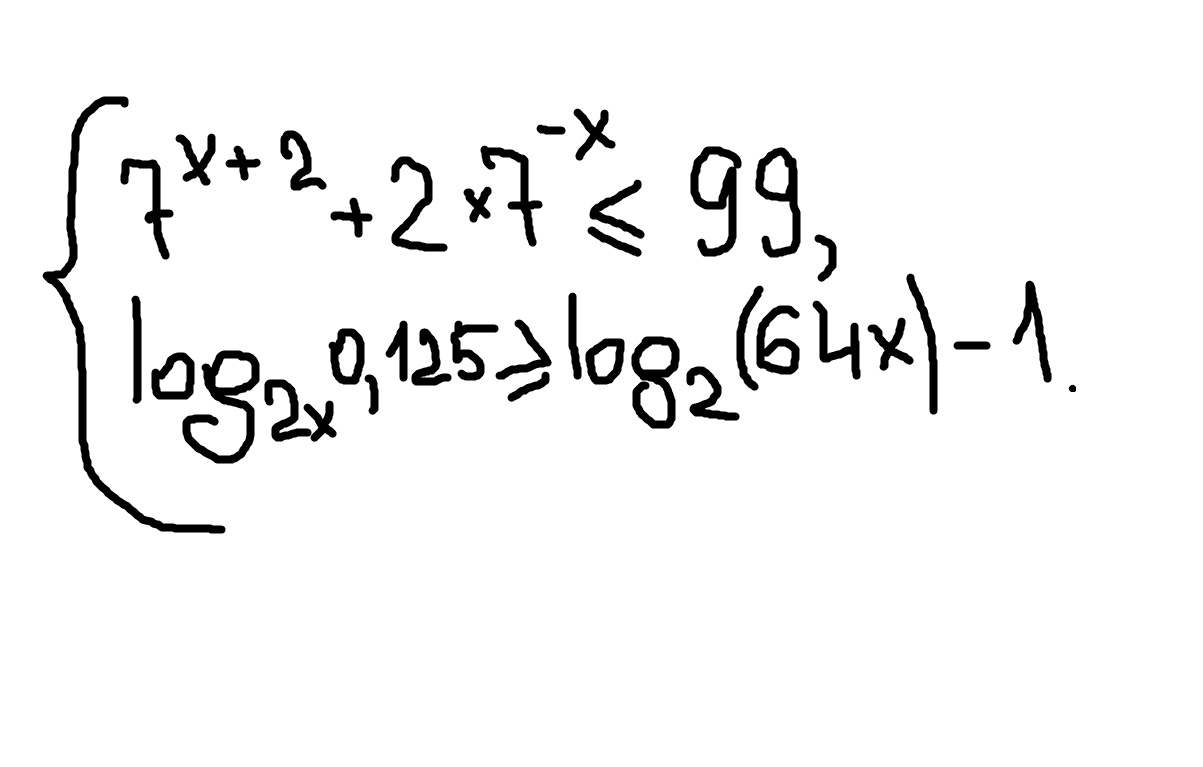Ответы
Ответ дал:
0
Решаем 1-ое неравенство, а потом второе.
![0<7^x leq 2\7^x leq 7^{log_7{2}}, x leq log_7{2}, log_7{2}=frac{lg2}{lg7}=0,36\2)log_{2x}0,125=log_{2x}{(frac{1}{2})^3}=log_{2x}{2^{-3}}=-3log_{2x}{2}=\=-3frac{1}{log_2{2x}}=frac{-3}{1+log_2x}\log_2(64x)=log_2(2^6x)=6log_2{2}+log_2x=6+log_2x\frac{-3}{1+log_2x}-6-log_2x+1 geq 0\y=log_2x, x>0,xne 1\frac{-3}{1+y}-y-5 geq 0\frac{-y^2-6y-8}{y+1} geq 0\frac{-(y+4)(y+2)}{y+1} geq 0, frac{(y+4)(y+2)}{y+1} leq 0\\ - - - - - - [-4]+++++++[-2]- - - - - -[-1]+++++](https://tex.z-dn.net/?f=0%26lt%3B7%5Ex+leq+2%5C7%5Ex+leq+7%5E%7Blog_7%7B2%7D%7D%2C+x+leq+log_7%7B2%7D%2C+log_7%7B2%7D%3Dfrac%7Blg2%7D%7Blg7%7D%3D0%2C36%5C2%29log_%7B2x%7D0%2C125%3Dlog_%7B2x%7D%7B%28frac%7B1%7D%7B2%7D%29%5E3%7D%3Dlog_%7B2x%7D%7B2%5E%7B-3%7D%7D%3D-3log_%7B2x%7D%7B2%7D%3D%5C%3D-3frac%7B1%7D%7Blog_2%7B2x%7D%7D%3Dfrac%7B-3%7D%7B1%2Blog_2x%7D%5Clog_2%2864x%29%3Dlog_2%282%5E6x%29%3D6log_2%7B2%7D%2Blog_2x%3D6%2Blog_2x%5Cfrac%7B-3%7D%7B1%2Blog_2x%7D-6-log_2x%2B1+geq+0%5Cy%3Dlog_2x%2C+x%26gt%3B0%2Cxne+1%5Cfrac%7B-3%7D%7B1%2By%7D-y-5+geq+0%5Cfrac%7B-y%5E2-6y-8%7D%7By%2B1%7D+geq+0%5Cfrac%7B-%28y%2B4%29%28y%2B2%29%7D%7By%2B1%7D+geq+0%2C+frac%7B%28y%2B4%29%28y%2B2%29%7D%7By%2B1%7D+leq+0%5C%5C+-+-+-+-+-+-+%5B-4%5D%2B%2B%2B%2B%2B%2B%2B%5B-2%5D-+-+-+-+-+-%5B-1%5D%2B%2B%2B%2B%2B%0A%0A "0<7^x leq 2\7^x leq 7^{log_7{2}}, x leq log_7{2}, log_7{2}=frac{lg2}{lg7}=0,36\2)log_{2x}0,125=log_{2x}{(frac{1}{2})^3}=log_{2x}{2^{-3}}=-3log_{2x}{2}=\=-3frac{1}{log_2{2x}}=frac{-3}{1+log_2x}\log_2(64x)=log_2(2^6x)=6log_2{2}+log_2x=6+log_2x\frac{-3}{1+log_2x}-6-log_2x+1 geq 0\y=log_2x, x>0,xne 1\frac{-3}{1+y}-y-5 geq 0\frac{-y^2-6y-8}{y+1} geq 0\frac{-(y+4)(y+2)}{y+1} geq 0, frac{(y+4)(y+2)}{y+1} leq 0\\ - - - - - - [-4]+++++++[-2]- - - - - -[-1]+++++")
![yin (-infty,-4]U[-2,-1]\log_2{x} leq -4,log_2{x} leq log_2{2^{-4}}, x leq frac{1}{16}\ left { {{log_2{x} geq -2} atop {log_2{x} leq {-1}} right. left { {{x leq frac{1}{4}} atop {x leq frac{1}{2}}} right.\xin (-infty,frac{1}{16}]U[frac{1}{4},frac{1}{2}]](https://tex.z-dn.net/?f=yin+%28-infty%2C-4%5DU%5B-2%2C-1%5D%5Clog_2%7Bx%7D+leq+-4%2Clog_2%7Bx%7D+leq+log_2%7B2%5E%7B-4%7D%7D%2C+x+leq+frac%7B1%7D%7B16%7D%5C+left+%7B+%7B%7Blog_2%7Bx%7D+geq+-2%7D+atop+%7Blog_2%7Bx%7D+leq+%7B-1%7D%7D+right.++left+%7B+%7B%7Bx+leq+frac%7B1%7D%7B4%7D%7D+atop+%7Bx+leq+frac%7B1%7D%7B2%7D%7D%7D+right.%5Cxin+%28-infty%2Cfrac%7B1%7D%7B16%7D%5DU%5Bfrac%7B1%7D%7B4%7D%2Cfrac%7B1%7D%7B2%7D%5D+ "yin (-infty,-4]U[-2,-1]\log_2{x} leq -4,log_2{x} leq log_2{2^{-4}}, x leq frac{1}{16}\ left { {{log_2{x} geq -2} atop {log_2{x} leq {-1}} right. left { {{x leq frac{1}{4}} atop {x leq frac{1}{2}}} right.\xin (-infty,frac{1}{16}]U[frac{1}{4},frac{1}{2}]")
Вывод:
![xin [frac{1}{4},log_7{2}]](https://tex.z-dn.net/?f=xin+%5Bfrac%7B1%7D%7B4%7D%2Clog_7%7B2%7D%5D "xin [frac{1}{4},log_7{2}]")
Вывод:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад