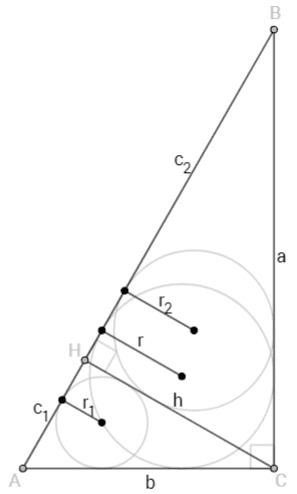
В прямоугольном треугольнике ABC ( угол C = 90° ) проведена высота СН = h. В треугольники ABC, ACH, BCH вписаны окружности радиусов r, r1, r2. Верно ли, что r+r1+r2=h?

Радиус вписанной окружности равен полуразности суммы катетов и гипотенузы.

BC=a; AC=b; AH=c1; BH=c2

r= (a +b -c1 -c2)/2
r1= (h +c1 -b)/2
r2= (c2 +h -a)/2

r +r1 +r2 =(a +b -c1 -c2 +h +c1 -b +c2 +h -a)/2 =2h/2 =h