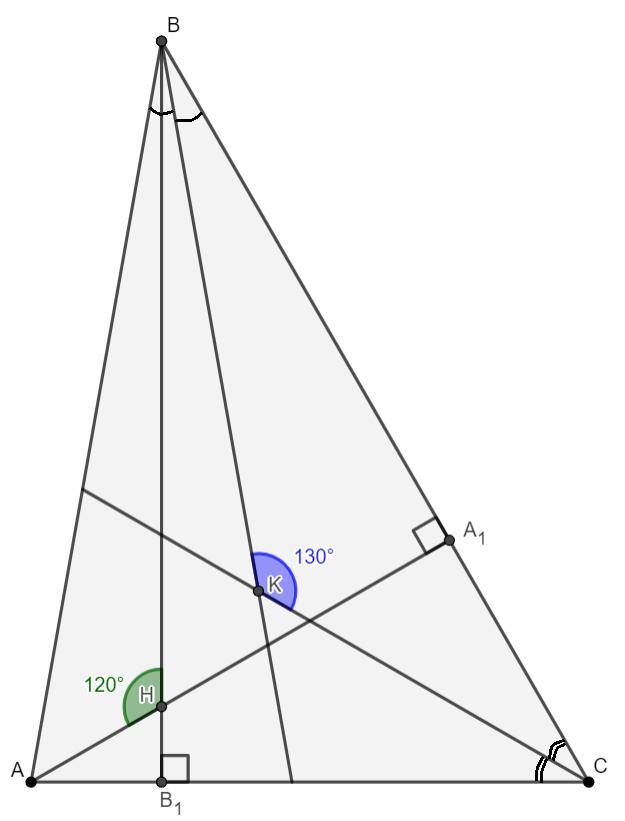
Высоты остроугольного треугольника ABC, про-
веденные из вершин A и B, пересекаются в точке H, при-
чем ∠AHB = 120◦, а биссектрисы, проведенные из вершин B
и C, в точке K, причем ∠BKC = 130◦. Найдите угол ABC.

Пусть АА₁ и ВВ₁ - высоты, ВВ₂ и СС₁ - биссектрисы.

1. Рассмотрим ΔВНА₁, <НА₁В=90°.

<ВНА₁=180°-120°=60°

<НВА₁=90°-60°=30° 

2. Рассмотрим ΔВКС

<КВС+<КСВ=180°-130°=50°

3. <В+<С=2·50°=100°

<А=180°-100°=80°

4. Рассмотрим ΔАВ₁В, <АВ₁В=90°.

<В₁ВА=90°-80°=10°

5. <АВС=<НВА₁+<В₁ВА=30°+10°=40°

Ответ. 40° 

Ответ:

∠ABC = 40°

Объяснение:

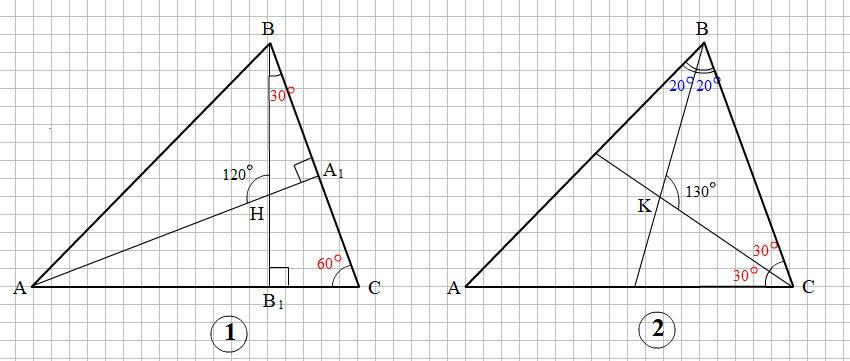
Смотри прикреплённый рисунок 1

∠ВА₁Н = 90°, так как АА₁ - высота.

∠АНВ = 120° - внешний угол при вершине Н для ΔА₁ВН

∠АНВ = ∠ВА₁Н + ∠НВА₁ ⇒ ∠НВА₁ = ∠АНВ - ∠ВА₁Н =120° - 90° = 30°.

В ΔВВ₁С  ∠ С = 90° - ∠НВА₁ = 90° - 30° - 60°.

Смотри прикреплённый рисунок 2

В ΔВКС ∠ ВСК = 0,5 ∠С = 0,5 · 60° = 30°, так как СК - биссектриса

По свойству углов треугольника

∠КВС = 180° - (∠ВКС + ∠ВСК) = 180° - (130° + 30°) = 20°.

∠АВС = 2 ∠КВС = 2 · 20° = 40°, так как ВК - биссектриса.

Биссектриса делит угол пополам, поэтому 2·∠KBC=∠ABC и 2·∠KCB=∠ACB.

В ΔKBC:

∠KBC+∠KCB=180°-∠CKB=180°-130°=50°.

В ΔABC:

∠BAC = 180°-(∠ABC+∠ACB) = 180°-(2·∠KBC+2·∠KCB) = 180°-2·50° = 80°

Пусть BB₁ ⊥ AC,  B₁∈AC.

В прямоугольном ΔAB₁B (∠B₁=90°):

∠ABB₁ = 90°-∠B₁AB = 90°-80° = 10°

Пусть AA₁ ⊥ BC,  A₁∈BC.

∠AHB и ∠BHA₁ смежные.

Поэтому ∠BHA₁ = 180°-∠AHB = 180°-120° = 60°

В прямоугольном ΔHA₁B (∠A₁=90°):

∠HBA₁ = 90°-∠BHA₁ = 90°-60° = 30°.

∠ABC = ∠ABH+∠HBA₁ = 10°+30° = 40°

Ответ: 40°.