Через конец радиуса шара проведена плоскость под углом 30 к нему. Найдите радиус полученного сечения, если радиус шара равен 1.

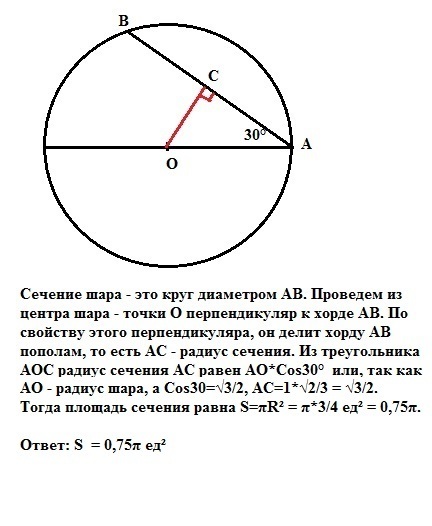
Искомое сечение шара - это круг диаметром АВ, наклоненным к диаметру шара под углом 30° (дано). Проведем из центра шара перпендикуляр ОС к хорде АВ. По свойству этого перпендикуляра он делит хорду АВ пополам, то есть АС - радиус сечения. Из прямоугольного треугольника АОС радиус АС равен АО*Cos30 или, так как АО - радиус шара, а Cos30=√3/2, АС=1*√2/3 = √3/2. Тогда площадь сечения равна S=πR² = π*3/4 ед² = 0,75π.

Ответ: S  = 0,75π ед²