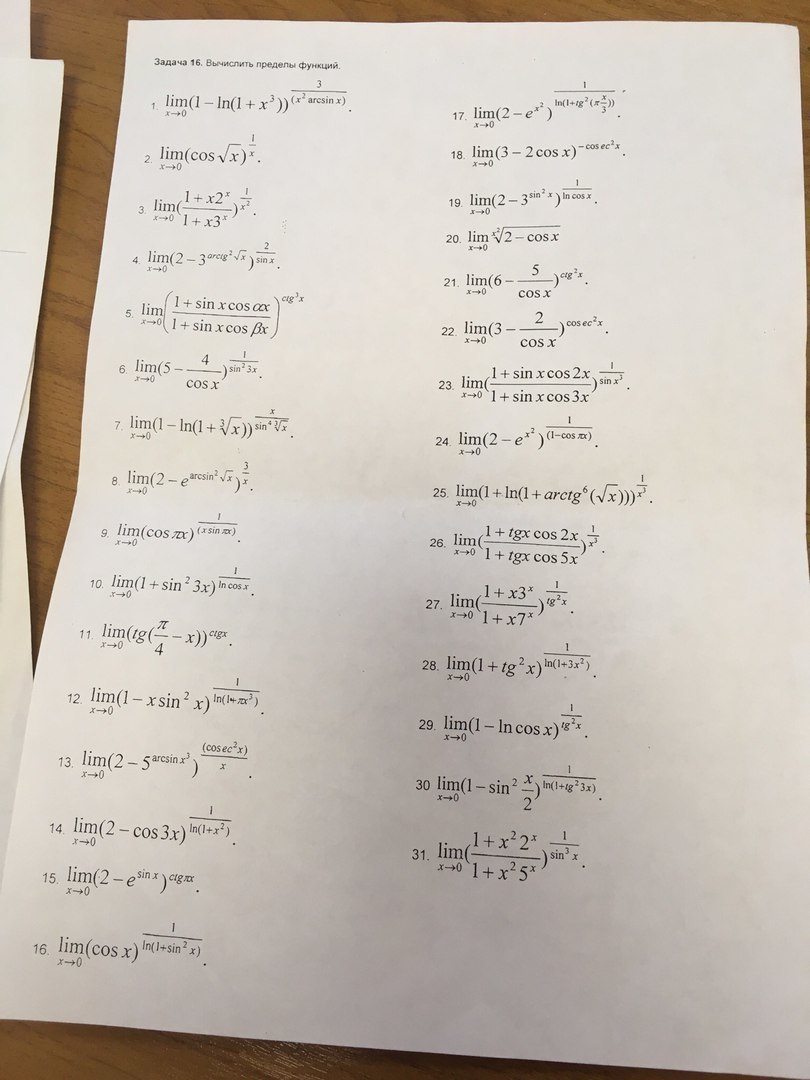Ответы
Ответ дал:
0
11. Неопределённость  (1 в степени бесконечность) раскрывается с помощью второго замечательного предела.
(1 в степени бесконечность) раскрывается с помощью второго замечательного предела.
Предварительно преобразуем тангенс суммы по формуле:



Вот этот предел и есть второй замечательный предел

Предварительно преобразуем тангенс суммы по формуле:
Вот этот предел и есть второй замечательный предел
Похожие вопросы
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад