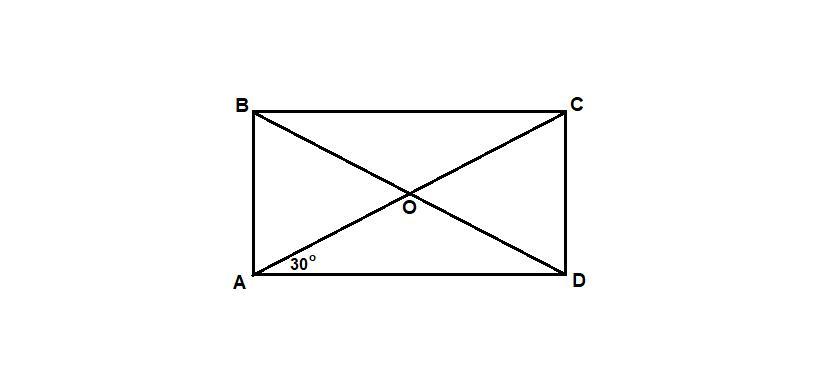
В прямоугольнике АВСД диагонали пересекаются в точке О. Найдите периметр треугольника АОВ, если угол САД = 30 градусов, АС = 12 см
Ответы
Ответ дал:
0
Ответ:
18 см
Объяснение:
Диагонали прямоугольника равны и точкой пересечения делятся пополам, значит
АО = ВО = АС/2 = 12/2 = 6 см
∠ВАС = ∠BAD - ∠CAD = 90° - 30° = 60°
ΔАВО равнобедренный с основанием АВ, значит углы при основании равны:
∠ВАО = ∠АВО = 60°
Так как сумма углов треугольника равна 180°, то ∠АОВ = 60°.
Значит ΔАОВ равносторонний (все углы равны).
Рaob = 3 · АО = 3 · 6 = 18 см
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
9 лет назад
9 лет назад