Найти боковые стороны равнобедренной трапеции,основания которой равны 34 см и 28 см,если один из углов 120 градусов

В трапеции сумма углов, прилежащих к боковой стороне=180°,
поэтому ∠Д=∠А=180-120=60°.
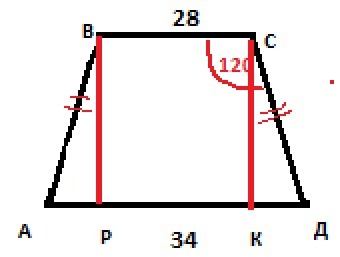
Опустим ВР⊥АД и СК⊥АД. Тогда АР=(АД-ВС)/2=3см.
В ΔАВР ∠АВР=90-60=30°, значит АВ=СД=АР*2=3*2=6см, так как катет, лежащий в прямоугольном треугольнике равен половине гипотенузы.
Ответ: АВ=СД=6см