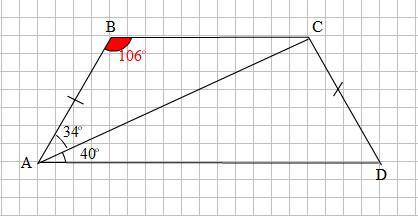
Найдите больший угол равнобедренной трапеции ABCD , если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 40° и 34° соответственно. Ответ дайте в градусах.
Ответы
Ответ дал:
0
Ответ:
106°
Объяснение:
Смотри рисунок на прикреплённом фото.
В трапеции АВСD ∠А = 40° + 34° = 74°.
Очевидно, что острый ∠А - меньший угол равнобедренной трапеции, как и ∠D = ∠A. Тогда большими углами являются ∠В = ∠С.
∠А + ∠B = 180° как углы, прилегающие к стороне АВ трапеции, тогда
∠В = 180° - ∠А = 180° - 74° = 106°.
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
9 лет назад
9 лет назад
9 лет назад