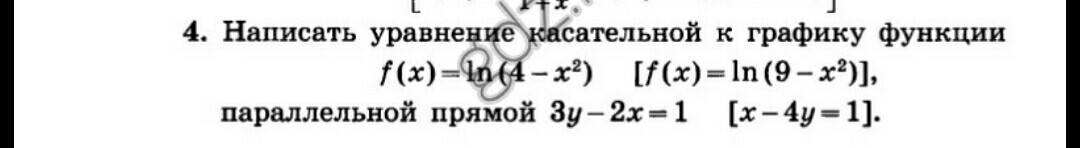Ответы
Ответ дал:
0
1) написать уравнение касательной.

и параллельной

Нам не дана точка касания.. Но это не проблема
Параллельность прямых означает равенство к-тов k (y=kx+b)
и т-нт k это значение производной в точке касания
найдем производную

приравняв ее значение 2/3 мы найдем точку касания

вроде бы получили две точки.. но не забываем проверить ОДЗ
(4-х²)>0; x²<4; -2<x<2
Так что у нас только одна точка х=-1
Теперь составим уравнение касательной


2) не так подробно



х=9 опять же не лежит в ОДЗ
тогда точка касания х=-1


и параллельной
Нам не дана точка касания.. Но это не проблема
Параллельность прямых означает равенство к-тов k (y=kx+b)
и т-нт k это значение производной в точке касания
найдем производную
приравняв ее значение 2/3 мы найдем точку касания
вроде бы получили две точки.. но не забываем проверить ОДЗ
(4-х²)>0; x²<4; -2<x<2
Так что у нас только одна точка х=-1
Теперь составим уравнение касательной
2) не так подробно
х=9 опять же не лежит в ОДЗ
тогда точка касания х=-1
Ответ дал:
0
спасибо вам онромное
Ответ дал:
0
огромное*
Ответ дал:
0
2x² -6x -8 = 0 , x₁ ≠ 8
Ответ дал:
0
task/26672000
---------------------
см приложение
---------------------
см приложение
Приложения:


Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
9 лет назад
9 лет назад
9 лет назад